思路：刚体可看成是连续质元组成的一个特殊的质点系，欲求刚体的角动量，可先求各个质元的角动量，然后按矢量运算方法将所有质元的角动量矢量相加而得。

　　 刚体定轴转动的角动量

　　为简单起见，现考察一均匀细棒绕固定轴OZ以角速度ω转动。 现将细棒分为许多质元，设第i个质元的质量为△m_i，当细棒转动时，此质元绕轴作半径为r_i的圆周运动。它相对于O点的角动量可由质点角动量定义式给出：

　　　　　　　　△L_i ＝l_i×△m_iV_i

　　l_i为O点到△m_i的矢径

　　V_i为△m_i的线速度。

　　由于V_i ⊥l_i

　　故︱△L_i︱＝△m_il_iV_i，方向如图△L_i方向，那么，刚体对O点的总角动量为：

　　　　　　L=∑△L_i=(L_i×△m_iv_i)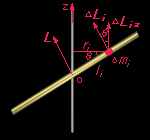

　　在讨论刚体定轴转动时， 刚体定轴转动对通过O点的Z轴的角动量 L_Z，就是各质元对O点的角动量沿Z轴的分量△L_iZ 的和。

　　△L_iZ＝△L_icosθ＝△m_il_icosθV_i＝△m_ir_i 　　V_i＝△m_il_i²ω　

　　L_Z＝△L_iZ＝(△m_ir_i²)ω＝J_zω　　

　　J_z称为刚体对Z轴的转动惯量

　　刚体定轴转动时对定轴的角动量 = 刚体对该轴的转动惯量 × 刚体对该轴转动角速度

思考：刚体定轴转动时对点的角动量与对轴的角动量两者关系如何？

例题：细杆定轴转动