1.磁化强度
仿照讨论电介质极化时定义极化强度的方法,引进一个表征磁介质磁化程度的宏观物理量,磁化强度。在被磁化后的磁介质内,任取一宏观小而微观大的体积元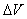 ,在这一体积元中所有分子固有磁矩的矢量和 ,在这一体积元中所有分子固有磁矩的矢量和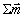 加上附加磁矩的矢量和 加上附加磁矩的矢量和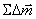 与该体积元的比值,即单位体积内分子磁矩的矢量和称为磁化强度,用 与该体积元的比值,即单位体积内分子磁矩的矢量和称为磁化强度,用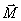 表示: 表示:
对于顺磁质, 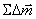 可以忽略;对于抗磁质, 可以忽略;对于抗磁质, 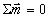 ,对于真空, ,对于真空,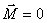 。 。
在磁介质被磁化后,介质内各点的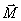 可以不同,这反映了不同点磁化程度的不同,是不均匀磁化,这可能是介质密度不均匀或外磁场强度不均匀引起的。如果在介质中各点的 可以不同,这反映了不同点磁化程度的不同,是不均匀磁化,这可能是介质密度不均匀或外磁场强度不均匀引起的。如果在介质中各点的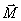 相同,就称磁介质被均匀磁化。在国际单位制中, 相同,就称磁介质被均匀磁化。在国际单位制中,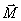 的单位是A/m. 的单位是A/m.
顺磁质经磁化后,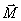 的方向与该处的磁场 的方向与该处的磁场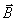 一致,它在磁介质内所激发的附加磁场的方向也与 一致,它在磁介质内所激发的附加磁场的方向也与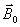 的方向相同。由此可见,顺磁质的磁化和有极分子的电极化有部分类似之处,两者都是起源于分子固有磁矩或固有电矩在外磁场或外电场中的取向作用。但是,两者所产生的效果又有不同之处,顺磁质磁化后激发在顺磁质内的附加磁场 的方向相同。由此可见,顺磁质的磁化和有极分子的电极化有部分类似之处,两者都是起源于分子固有磁矩或固有电矩在外磁场或外电场中的取向作用。但是,两者所产生的效果又有不同之处,顺磁质磁化后激发在顺磁质内的附加磁场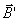 与外磁场 与外磁场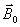 同向,使总场增强,而电介质电极化后激发在电介质内的附加电场 同向,使总场增强,而电介质电极化后激发在电介质内的附加电场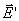 却总是与外电场 却总是与外电场 反向,使总场减弱。 反向,使总场减弱。
抗磁质经磁化后,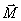 的方向与该处磁场 的方向与该处磁场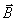 相反,它在磁介质内所激发的附加磁场 相反,它在磁介质内所激发的附加磁场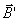 的方向也与 的方向也与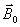 的方向相反。由此可见,抗磁质的磁化与无极分子的电极化完全类似,分子磁矩或分子电矩都是在外磁场或外电场中产生的,在介质内部的附加磁场或附加电场的方向也都与外磁场或外电场的方向相反,使总场减弱。 的方向相反。由此可见,抗磁质的磁化与无极分子的电极化完全类似,分子磁矩或分子电矩都是在外磁场或外电场中产生的,在介质内部的附加磁场或附加电场的方向也都与外磁场或外电场的方向相反,使总场减弱。
2.磁化电流
在外磁场中,磁化了的磁介质会激发附加磁场。该附加磁场起源于磁化了的介质内所出现的磁化电流(实质上是分子电流的宏观表现)。这样,一个磁介质的磁化情况,可以用磁化强度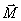 来描述,也可以用磁化电流来反映,两者之间必然存在一定的联系。我们将用直观的方法找出能测定的宏观的磁化强度与磁化电流之间的关系。 来描述,也可以用磁化电流来反映,两者之间必然存在一定的联系。我们将用直观的方法找出能测定的宏观的磁化强度与磁化电流之间的关系。
为方便计,我们选一特例来讨论。设有一“无限长”的载流直螺线管,管内充满均匀磁介质,电流在螺线管内激发匀强磁场。在此磁场中磁介质被均匀磁化,这时磁介质中各个分子电流平面将转到与磁场的方向相垂直,图8-42表示磁介质内任一截面上分子电流排列的情况。从图8-42(c)和(d)中可以看出,在磁介质内部任意一点处,总是有两个方向相反的分子电流通过,结果相互抵消;只有在截面边缘处,分子电流未被抵消,形成与截面边缘重合的圆电流。对磁介质的整体来说,未被抵消的分子电流是沿着柱面流动的,称为安培表面电流(或叫磁化面电流)。对顺磁性物质,安培表面电流和螺线管上导线中的电流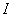 方向相同;对抗磁性物质,则两者方向相反。图8-42所示是顺磁质的情况。 方向相同;对抗磁性物质,则两者方向相反。图8-42所示是顺磁质的情况。 |
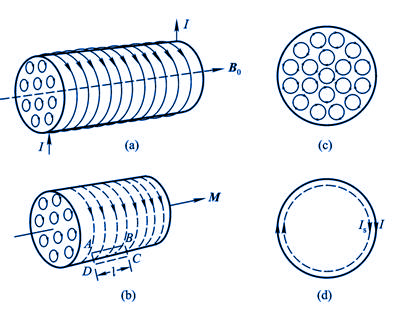
图8-42 |
3.磁化电流与磁化强度的关系
设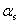 为圆柱形磁介质表面上“单位长度的磁化面电流”, 为圆柱形磁介质表面上“单位长度的磁化面电流”,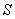 为磁介质的截面积, 为磁介质的截面积,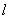 为所选取的一段磁介质的长度。在 为所选取的一段磁介质的长度。在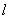 长度上,表面电流的总量值为 长度上,表面电流的总量值为 ,因此在这段磁介质总体积 ,因此在这段磁介质总体积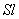 中的总磁矩为 中的总磁矩为
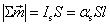
按定义,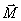 为单位体积内的磁矩,所以 为单位体积内的磁矩,所以
即磁介质表面某处单位长度的磁化面电流的大小等于该处磁化强度的量值,这和电介质中极化强度与极化面电荷的关系相似。上述结果是从均匀磁介质被均匀磁化的特例导出的,在一般情况中,应该是磁介质表面上某处单位长度的磁化面电流(即磁化面电流的线密度)等于该处磁化强度的切线分量。而且在不均匀磁介质内部,由于排列着的分子电流未能相互抵消,此时磁体内各点都有磁化电流。
磁化电流可写成矢量式为:
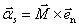
式中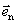 为介质表面的法线方向单位矢量。 为介质表面的法线方向单位矢量。
式(8-117)表明了磁介质表面上某点的磁化面电流与该点处磁化强度的关系,下面进一步讨论通过任一曲面的磁化电流与磁化强度的联系,为此我们仍用前述特例计算磁化强度对闭合回路的线积分 与磁化电流的关系。 与磁化电流的关系。
在图8-42(b)所示的圆柱形磁介质的边界附近,取一长方形闭合回路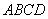 , ,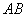 边在磁介质内部,它平行于柱体轴线,长度为 边在磁介质内部,它平行于柱体轴线,长度为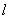 ,而 ,而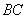 、 、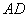 两边则垂直于柱面。在磁介质内部各点处, 两边则垂直于柱面。在磁介质内部各点处,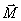 都沿 都沿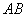 方向,大小相等,在柱外各点处 方向,大小相等,在柱外各点处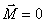 。所以 。所以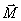 沿 沿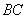 、 、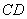 、 、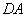 三边的积分为零,因而 三边的积分为零,因而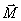 对闭合回路 对闭合回路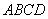 的积分等于 的积分等于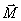 沿 沿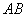 边的积分,即 边的积分,即
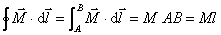
将式(8-117) 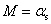 代人后得 代人后得
这里,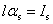 就是通过以闭合回路 就是通过以闭合回路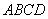 为边界的任意曲面的总磁化电流,所以式(8-118)表明磁化强度对闭合回路的线积分等于通过回路所包围的面积内的总磁化电流。要说明的是:式(8-118)虽是从均匀磁化介质及长方形闭合回路的简单特例导出的,但却是在任何情况都普遍适用的关系式。 为边界的任意曲面的总磁化电流,所以式(8-118)表明磁化强度对闭合回路的线积分等于通过回路所包围的面积内的总磁化电流。要说明的是:式(8-118)虽是从均匀磁化介质及长方形闭合回路的简单特例导出的,但却是在任何情况都普遍适用的关系式。
4.有磁介质时的安培环路定理
当电流的磁场中有磁介质存在时,空向任一点的磁感应强度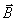 等于导线中传导电流所激发的磁场与磁介质磁化后磁化电流所激发的附加磁场的矢量和,这时安培环路定理应写成 等于导线中传导电流所激发的磁场与磁介质磁化后磁化电流所激发的附加磁场的矢量和,这时安培环路定理应写成
等式右边的两项电流是穿过以回路为边界的任一曲面的总电流,即传导电流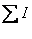 和磁化电流 和磁化电流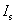 的代数和。一般说来, 的代数和。一般说来,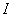 是可以测量的,可认为它是已知的;而 是可以测量的,可认为它是已知的;而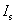 不能事先给定,也无法直接测量,它依赖于介质磁化的情况,而介质的磁化情况又依赖于磁介质中的磁感应强度 不能事先给定,也无法直接测量,它依赖于介质磁化的情况,而介质的磁化情况又依赖于磁介质中的磁感应强度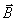 ,因此直接求解方程(8-119)很复杂。为了解决这一困难,我们利用关系式(8-118)将式(8-119)可改写成 ,因此直接求解方程(8-119)很复杂。为了解决这一困难,我们利用关系式(8-118)将式(8-119)可改写成
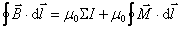
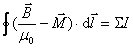
然后采取和电介质中引进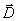 矢量相似的方法,引进一个新的物理量,称为磁场强度,用符号 矢量相似的方法,引进一个新的物理量,称为磁场强度,用符号 表示(通常称为 表示(通常称为 矢量),定义为
这样,便有下列简单的形式
式(8-121)称为有磁介质时的安培环路定理,它表明 矢量),定义为
这样,便有下列简单的形式
式(8-121)称为有磁介质时的安培环路定理,它表明 矢量的环流只和传导电流 矢量的环流只和传导电流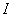 有关,而在形式上与磁介质的磁性无关。这就是说,当传导电流 有关,而在形式上与磁介质的磁性无关。这就是说,当传导电流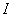 给定以后,不论磁场中放进什么样的磁介质或者同一块磁介质放在不同的地方,虽然在不同情况下空间同一点的 给定以后,不论磁场中放进什么样的磁介质或者同一块磁介质放在不同的地方,虽然在不同情况下空间同一点的 矢量有所不同,但 矢量有所不同,但 矢量的环流只和传导电流有关。因此引人磁场强度 矢量的环流只和传导电流有关。因此引人磁场强度 这个物理量以后,在磁场分布具有高度对称性时,能够使我们比较方便地处理有磁介质时的磁场问题,就象引人电位移矢量 这个物理量以后,在磁场分布具有高度对称性时,能够使我们比较方便地处理有磁介质时的磁场问题,就象引人电位移矢量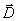 后使我们能够比较方便地处理有电介质时的静电场问题一样。安培环路定理[式(8-121)〕和静磁场的另一普遍规律——磁场中的高斯定理 后使我们能够比较方便地处理有电介质时的静电场问题一样。安培环路定理[式(8-121)〕和静磁场的另一普遍规律——磁场中的高斯定理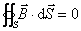 一起,是处理静磁场问题的基本定理。 一起,是处理静磁场问题的基本定理。
在国际单位制中,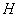 的单位是 的单位是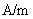 。 。
5.各向同性磁介质中各量之间的关系
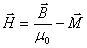 表示了磁介质中任一点处磁感应强度 表示了磁介质中任一点处磁感应强度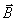 、磁场强度 、磁场强度 和磁化强度 和磁化强度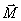 之间的普遍关系,不论磁介质是否均匀,甚至对铁磁性物质都能适用,通常写成 之间的普遍关系,不论磁介质是否均匀,甚至对铁磁性物质都能适用,通常写成
显然,磁化强度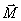 不仅和磁介质的性质有关,也和磁介质所在处的磁场有关,实验证明,对于各向同性的磁介质,在磁介质中任一点磁化强度 不仅和磁介质的性质有关,也和磁介质所在处的磁场有关,实验证明,对于各向同性的磁介质,在磁介质中任一点磁化强度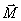 和磁场强度 和磁场强度 成正比,即
式中比例系数 成正比,即
式中比例系数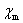 只与磁介质的性质有关,称为磁介质的磁化率。因为 只与磁介质的性质有关,称为磁介质的磁化率。因为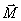 和 和 所用的单位相同,所以磁化率 所用的单位相同,所以磁化率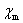 是单位为1的量。如果磁介质是均匀的,则是常量;如果磁介质是不均匀的,则 是单位为1的量。如果磁介质是均匀的,则是常量;如果磁介质是不均匀的,则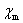 是空间位置的函数。对于顺磁质, 是空间位置的函数。对于顺磁质,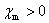 ,磁化强度 ,磁化强度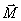 和磁场强度 和磁场强度 的方向相同;对于抗磁质, 的方向相同;对于抗磁质, 磁化强度 磁化强度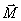 和磁场强度 和磁场强度 的方向相反。把式(8-123)代人式(8-122a)中可得
通常令 的方向相反。把式(8-123)代人式(8-122a)中可得
通常令
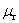 称为该磁介质的相对磁导率。于是式(8-124)成为
式中 称为该磁介质的相对磁导率。于是式(8-124)成为
式中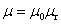 称为磁介质的磁导率。对于真空中的磁场来说,由于 称为磁介质的磁导率。对于真空中的磁场来说,由于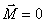 ,从式(8-122a)得到 ,从式(8-122a)得到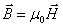 ,这表明“真空”相当于 ,这表明“真空”相当于 的“磁介质”。真空中各点处的磁场强度 的“磁介质”。真空中各点处的磁场强度 等子该点磁感强度的 等子该点磁感强度的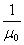 倍,即 倍,即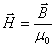 。 。
对于各向同性的磁介质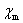 是常量, 是常量,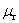 也是常量,且都是无单位的量, 也是常量,且都是无单位的量,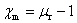 。磁介质的磁化率 。磁介质的磁化率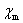 、相对磁导率 、相对磁导率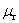 、磁导率 、磁导率 都是描述磁介质磁化特性的物理量,只要知道三个量中的任一个量,该介质的磁性就完全清楚了。 都是描述磁介质磁化特性的物理量,只要知道三个量中的任一个量,该介质的磁性就完全清楚了。
所有顺磁牲、抗磁性材料的磁化率的值都很小,其相对磁导率几乎等于1,这说明它们对电流的磁场只产生微弱的影响。
对子铁磁质来说,铁磁质中任一点处的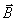 、 、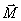 、 、 三矢量之间的普遍关系仍采用定义式(8-122a),但是,实验发现铁磁质中 三矢量之间的普遍关系仍采用定义式(8-122a),但是,实验发现铁磁质中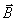 与 与 以及 以及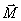 与 与 之间并没有线性的正比关系,甚至不存在单值关系,虽然在形式上仍引用式(8-123)和式(8-126),但式中铁磁质的磁导率 之间并没有线性的正比关系,甚至不存在单值关系,虽然在形式上仍引用式(8-123)和式(8-126),但式中铁磁质的磁导率 相对磁导率 相对磁导率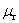 和磁化率 和磁化率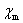 都不是常量。在§8-9中,将从实验出发讨论铁磁性物质的磁化特性,并介绍形成这种独特特性的内在机制。 都不是常量。在§8-9中,将从实验出发讨论铁磁性物质的磁化特性,并介绍形成这种独特特性的内在机制。
6. 线 线
为了能形象地表示出磁场中 矢量的分布,类似于用磁感应线描述磁场的方法,我们也可以引人 矢量的分布,类似于用磁感应线描述磁场的方法,我们也可以引人 线来描述磁场, 线来描述磁场, 线与 线与 矢量的关系规定如下: 矢量的关系规定如下: 线上任一点的切线方向和该点 线上任一点的切线方向和该点 矢量的方向相同, 矢量的方向相同, 线的密度(即在与 线的密度(即在与 矢量垂直的单位面积上通过的 矢量垂直的单位面积上通过的 线数目)和该点 线数目)和该点 矢量的大小相等。从式(8-126)可见,在各向同性的均匀磁介质中,通过任何截面的磁感应线的数目是通过同一截面 矢量的大小相等。从式(8-126)可见,在各向同性的均匀磁介质中,通过任何截面的磁感应线的数目是通过同一截面 线的 线的 倍。 倍。
7.电介质与磁介质的比较
电介质与磁介质的比较
|
电介质 |
磁介质(非铁介质) |
现象 |
极化现象:电介质中的有极分子和无极分子在外电场作用下发生转向极化和位移极化,在介质表面出现极化电荷。 |
磁化现象:在外磁场作用下,磁介质中的分子电流的磁矩在一定程度上沿着磁场方向排列或和分子附加磁矩与外磁场反向排列,在介质表面出现束缚电流。 |
微观模型 |
分子电矩  |
分子磁矩 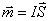 |
描述状态的物理量 |
电极化强度 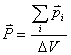 |
|
宏观效果 |
|
|
介质对场的影响
|
极化电荷的场强为 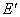
|
磁化分子面电流产生的磁场为 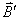
|
辅助物理量 |
电位移矢量 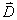
|
磁场强度 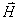
|
基本场方程 |
|
|
极化和磁化规律 |
|
|
参量间基本关系 |
|
|
边值关系 |
|
|
|