1.自感现象
我们知道,当回路中通有电流时,就有这一电流所产生的磁通量通过该回路本身,如果回路中的电流、或回路的形状、或回路周围的磁介质发生变化时,通过自己回路面积的磁通量也将发生变化,相应地,在自己回路中也将激起感应电动势,这种由于回路中电流产生的磁通量发生变化,而在自己回路中激起感应电动势的现象,称为自感现象,相应的电动势称为自感电动势。
下面用一个简单的例子讨论自感电动势的大小与哪些因素有关。设有一无铁芯的长直螺线管,长为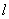 ,截面半径为 ,截面半径为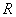 ,管上绕组的总匝数为 ,管上绕组的总匝数为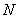 ,其中通有电流 ,其中通有电流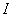 。对于一根密绕线圈的细长的螺线管,可以忽略漏磁和管两端磁场的不均匀性,把磁场近似地看做在管内均匀分布,此时线圈内各点的磁感应强度是 。对于一根密绕线圈的细长的螺线管,可以忽略漏磁和管两端磁场的不均匀性,把磁场近似地看做在管内均匀分布,此时线圈内各点的磁感应强度是
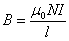
用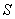 表示螺线管的截面积,则穿过每匝线圈的磁通量 表示螺线管的截面积,则穿过每匝线圈的磁通量
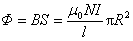
穿过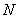 匝线圈的磁链数为 匝线圈的磁链数为
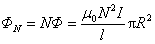
当线圈中的电流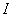 变化时,在 变化时,在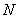 匝线圈中产生的感应电动势为 匝线圈中产生的感应电动势为
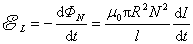
将上式改写成下列形式
式(9-12)反映了自感电动势与电流变化率之间的关系,其中的负号表明:当线圈回路中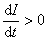 时, 时,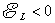 ,即自感电动势与电流方向相反;反之,当 ,即自感电动势与电流方向相反;反之,当 时, 时,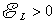 ,即自感电动势与电流方向相同。而式中的 ,即自感电动势与电流方向相同。而式中的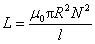 则体现回路产生自感电动势来反抗电流改变的能力,它称为该回路的自感系数,简称自感。 则体现回路产生自感电动势来反抗电流改变的能力,它称为该回路的自感系数,简称自感。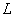 的大小与回路的几何形状、匝数等因素有关,所以如同电阻和电容一样,自感也是一个电路参数。 的大小与回路的几何形状、匝数等因素有关,所以如同电阻和电容一样,自感也是一个电路参数。
现在再考虑一般的情况。对于一个任意形状的回路,回路中由于电流变化引起通过回路本身磁链数的变化而出现的感应电动势为
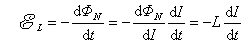
式中
便定义为回路的自感。它等于回路中的电流变化为单位值时,在回路本身所围面积内引起磁链数的改变值。如果回路的几何形状保持不变,而且在它的周围空间没有铁磁性物质,那么根据毕奥-萨伐尔定律,空间任一点的磁场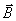 与回路中的电流 与回路中的电流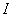 成正比,通过回路所围面积的磁链数 成正比,通过回路所围面积的磁链数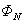 也与 也与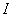 成正比,这时式(9-13)可写成
式(9-14)可作为不存在铁磁性物质时回路自感的定义,即回路自感的大小等于回路中的电流为单位值时通过这回路所围面积的磁链数,它仅与回路本身的几何结构及周围介质分布等因素有关,而和回路中的电流无关。如果回路周围有铁磁性物质存在,则通过回路所围面积的磁链数和回路中的电流 成正比,这时式(9-13)可写成
式(9-14)可作为不存在铁磁性物质时回路自感的定义,即回路自感的大小等于回路中的电流为单位值时通过这回路所围面积的磁链数,它仅与回路本身的几何结构及周围介质分布等因素有关,而和回路中的电流无关。如果回路周围有铁磁性物质存在,则通过回路所围面积的磁链数和回路中的电流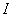 不呈线性关系,在这种情况下,从自感的一般定义式(9-13)可知,回路的自感 不呈线性关系,在这种情况下,从自感的一般定义式(9-13)可知,回路的自感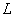 与电流 与电流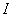 有关,也不是常量。
在国际单位制中,自感的单位为亨利,用符号 有关,也不是常量。
在国际单位制中,自感的单位为亨利,用符号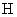 表示。由式(9-13)可知, 表示。由式(9-13)可知,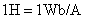 。由于亨利的单位比较大,实用上常用毫亨( 。由于亨利的单位比较大,实用上常用毫亨(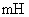 )与微亨( )与微亨(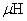 )作为自感的单位。 )作为自感的单位。
在日光灯上装置的镇流器和无线电技术、电工中使用的扼流圈是利用自感效应的常见实例。
2.互感现象
设有两个邻近的回路,其中分别通有电流,则任一回路中电流所产生的磁感应线将有一部分通过另一个回路所包围的面积,当其中任意一个回路中的电流发生变化时,通过另一个回路所围面积的磁通量也随之变化,因而在回路中产生感应电动势;这种由于一个回路中的电流变化而在邻近另一个回路中产生感应电动势的现象,称为互感现象。互感现象与自感现象一样,都是由电流变化而引起的电磁感应现象,所以可用讨论用互感现象类似的方法来进行研究。
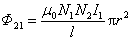
当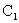 线圈中的电流 线圈中的电流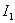 变化时,在 变化时,在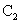 线圈中将产生感应电动势 线圈中将产生感应电动势
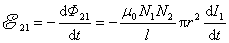
将上式改写成下列形式
式中 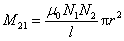 。 。
同样,当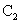 线圈中所通有的电流 线圈中所通有的电流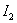 变化时,在 变化时,在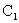 线圈回路中也将产生感应电动势
式(9-15)和(9-16)是互感电动势与电流变化率之间的关系,而且 线圈回路中也将产生感应电动势
式(9-15)和(9-16)是互感电动势与电流变化率之间的关系,而且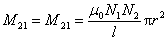 。可以证明,对于任意形状的两个回路,总是有 。可以证明,对于任意形状的两个回路,总是有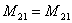 的关系,因此统一用符号 的关系,因此统一用符号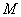 来表示,它反映了两个相邻回路各在另一回路中产生感应电动势的能力,称为两个回路的互感系数,简称互感。 来表示,它反映了两个相邻回路各在另一回路中产生感应电动势的能力,称为两个回路的互感系数,简称互感。
如果两个回路的相对位置固定不变,而且在其周围没有铁磁性物质,则两个回路的互感等于其中一个回路中单位电流激发的磁场通过另一回路所围面积的磁链数,即
在这种情况下,互感和自感以一只和两个回路的形状、相对位置及周围介质的磁导率有关,而与电流无关。
如果回路周围有铁磁性物质存在,那么通过其中任一回路的磁磁链数(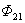 或 或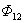 )和另外一个回路中的电流( )和另外一个回路中的电流(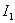 或 或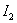 )没有简单线形正比关系,这时互感电动势为
或
式中 )没有简单线形正比关系,这时互感电动势为
或
式中 就作为互感的定义,它等于一回路中的电流改变单位值时,在另一回路所围面积中引起磁链数的改变值。这时,互感的值除和两个回路的形状、相对位置有关外,还和电流有关,也不再是常量。 就作为互感的定义,它等于一回路中的电流改变单位值时,在另一回路所围面积中引起磁链数的改变值。这时,互感的值除和两个回路的形状、相对位置有关外,还和电流有关,也不再是常量。
互感的单位也是亨利。
下面仍以图9-21的两层螺线管为例,说明两个回路各自的自感和互感的关系。由前面的讨论可知原线圈的自感
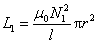
同理,副线圈的自感系数
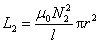
由此可见
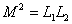 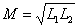
互感现象是在一些电器及电子线路中时常遇到的现象,有些电器利用互感现象把电能从一个回路输送到另一个回路中去,例如变压器及感应圈等。有时互感现象也会带来不利的一面,例如收音机各回路之间、电话线与电力输送线之间会因互感现象产生有害的干扰,了解了互感现象的物理本质,就可以设法改变电器间的布置,以尽量减小回路间相互磁耦合的影响。
形状不规则的回路系,互感一般不易计算,通常用实验方法来测定,但对于一些形状规则的回路系,仍能计算求得。 |