在电场中的电荷受到电场力的作用,移动电荷电场力要作功,这说明电场蕴藏着一定的能量——静电能。电容器放电时,常伴随有热、光、声等现象的产生,这就是电容器储存的电场能转化为其他形式能量的
设电容器的电容为C,此时电容器的带电量为q,则 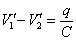 ,所以 ,所以
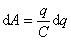
因此当电容器从 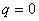 开始充电到带有电荷量 开始充电到带有电荷量 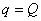 时,外力所作的总功为 时,外力所作的总功为
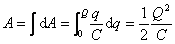
这个功应等于带电电容器的静电能。利用关系式 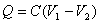 ,带电电容器的静电能W 又可写为 ,带电电容器的静电能W 又可写为
下面我们将进一步说明电容器的静电能也就是电场的能量,而且分布在电场所占的整个空间之中。
设平行板电容器极板的面积为S,两极板间的距离为d,当电容器极板上的电荷量为Q时,极板间的电势差  ,已知 ,已知 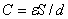 ,将这些关系式代入式(7-67)中,得 ,将这些关系式代入式(7-67)中,得
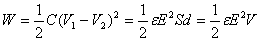
由此可见,静电能可以用表征电场性质的电场强度E 来表示,而且和电场所占的体积V=Sd 成正比。这表明电能储存在电场中。由于平板电容器中电场是均匀分布在两板之间的空间中,所贮藏的静电场能量也应该是均匀分布在电场所占的体积中,因此电场中每单位体积的能量,即电场能量密度为
能量密度的单位为J/m3。上述结果是从平行板电容器均匀电场的特例中导出的,在一般情况下,电场能量密度为
在各向同性线性介质中, 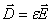 ,电场能量密度为
上述电场能量密度的表达式在非均匀电场和变化的电磁场中仍然是正确的,只是此时的能量密度是逐点改变的。要计算任一带电系统整个电场中所储存的总能量,只要将电场所占空间分成许多体积元dV,然后把这许多体积元中的能量累加起来,也就是求如下的积分
式中积分区域遍及整个电场空间V。 ,电场能量密度为
上述电场能量密度的表达式在非均匀电场和变化的电磁场中仍然是正确的,只是此时的能量密度是逐点改变的。要计算任一带电系统整个电场中所储存的总能量,只要将电场所占空间分成许多体积元dV,然后把这许多体积元中的能量累加起来,也就是求如下的积分
式中积分区域遍及整个电场空间V。
在公式(7-67)中静电能是由电荷量来表示的,似乎电荷是能量的携带者,而式(7-68)~式(7-71)又表明,静电能也可用电场强度来表出,这又表明静电能是储存于电场中,电场是电能的携带者。在静电场中,电荷和电场都不变化,而电场总是伴随着电荷而存在,因此我们无法用实验来检验电能究竟是以哪种方式储存的。但是在交变电磁场的实验中,已经证明了变化的场可以脱离电荷独立存在,而且场的能量是能够以电磁波的形式在空间传播的,这就直接证实了能量储存在场中的观点。能量是物质固有的属性之一,静电场具有能量的结论,证明静电场是一种特殊形态的物质。 |






