从理想气体分子的平均平动动能的公式
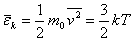
出发,考虑到大量气体分子作杂乱无章的运动时,各个方向运动的机会均等的统计假设,我们有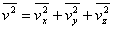 ,且 ,且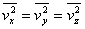 ,所以 ,所以
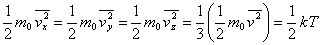
上式表明,气体分子沿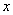 , ,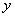 , ,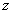 三个方向运动的平均平动动能完全相等;可以认为,分子的平均平动动能 三个方向运动的平均平动动能完全相等;可以认为,分子的平均平动动能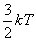 是均匀地分配在每一个平动自由度上的。因为分子平动有3个自由度,所以相应于每一个平动自由度的能量是 是均匀地分配在每一个平动自由度上的。因为分子平动有3个自由度,所以相应于每一个平动自由度的能量是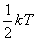 。 。
这个结论可以推广到刚性气体分子的转动上去。在平衡状态时,由于分子间频繁的无规则碰撞,平均地说,不论何种运动,相应于每一自由度的能量都应该相等。气体分子任一自由度的平均能量都等于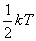 。如果气体分子有 。如果气体分子有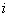 个自由度,则每个分子的总平均动能就是 个自由度,则每个分子的总平均动能就是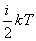 。能量按照这样分配的原则,叫做能量均分定理,这个原则是关于分子无规则运动动能的统计规律,是大量分子统计平均所得出的结果,也是分子热运动统计性的一种反映。如果气体分子不是刚性的,那么,除上述平动与转动自由度以外,还存在着振动自由度。对应于每一个振动自由度,每个分子除有 。能量按照这样分配的原则,叫做能量均分定理,这个原则是关于分子无规则运动动能的统计规律,是大量分子统计平均所得出的结果,也是分子热运动统计性的一种反映。如果气体分子不是刚性的,那么,除上述平动与转动自由度以外,还存在着振动自由度。对应于每一个振动自由度,每个分子除有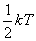 的平均动能外,还具有 的平均动能外,还具有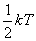 的平均势能,在每个振动自由度上将分配到量值为 的平均势能,在每个振动自由度上将分配到量值为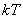 的平均能量。 的平均能量。
实际气体的分子运动情况视气体的温度而定。例如氢分子,在低温时,只可能有平动,在室温时,可能有平动和转动,只有在高温时,才可能有平动、转动和振动。又例如氯分子,在室温时已可能有平动、转动和振动。
|