1.力矩的功

当质点在外力作用下发生位移时，力就对质点作了功。与之相似，刚体在外力矩作用下转动时，力矩也对刚体做功。在刚体转动时，作用力可以作用在刚体的不同质点上，各个质点的位移也不相同。只有将各个力对各个相应质点作的功加起来，才能求得力对刚体所作的功。由于在转动的研究中，使用角量比使用线量方便，因此在功的表达式中力以力矩的形式出现，力作的功也就是力矩的功。其表达式为
            

式中为刚体所受到的总外力矩。因此，力矩的功即力矩与刚体角位移乘积的积分。

2.定轴转动的动能定理

根据定轴转动定理
            
    为了简化书写，把写成，则物体在时间内转过角位移时，外力矩所做元功为：
             
    如刚体的角速度由时刻的变为时刻的，则在此过程中总外力矩对刚体所作的功为
            

上式表明，总外力矩对刚体所作的功等于刚体转动动能的增量，这个关系式叫做刚体定轴转动的动能定理。

3.刚体的重力势能

如果一个刚体受到保守力的作用，也可引入势能的概念。刚体在定轴转动中涉及的势能主要是重力势能。这里把刚体-地球系统的重力势能简称刚体的重力势能，意思是取地面坐标系来计算势能值。

对于一个不太大的质量为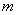的刚体，它的重力势能应是组成刚体的各个质点的重力势能之和，即
            

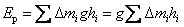
根据质心的定义，此刚体的质心的高度应为
            

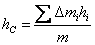
所以上式可改写为
            

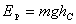
这一结果表明，一个不太大的刚体的重力势能与它的质量集中在质心时所具有的势能一样。
    考虑了刚体的功和能的上述特点，关于一般质点系统的功能原理、机械能守恒定律等，都可方便地用于刚体的定轴转动。