刚体的定轴转动定律可通过牛顿第二定律推得,其表达式为
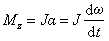
上式表明,刚体在总外力矩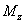 的作用下所获得的角加速度 的作用下所获得的角加速度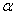 与总外力矩的大小成正比,并与转动惯量成反比,这个关系叫做刚体的定轴转动定律。 与总外力矩的大小成正比,并与转动惯量成反比,这个关系叫做刚体的定轴转动定律。
利用刚体对轴角动量的表达式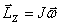 ,可将刚体的定轴转动定律改写成 ,可将刚体的定轴转动定律改写成
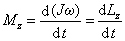
上式表示,刚体所受到的对某给定轴的总外力矩等于刚体对该轴的角动量的时间变化率。这是用角动量陈述的定轴转动定律。
应该注意,对于刚体来说,它对给定轴的转动惯量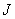 是保持不变的,因此转动定律的两种表达式的意义完全一样。但在实际中,用角动量陈述的定轴转动定律适用范围更为广泛,可以适用于刚体,也可以适用于非刚体。当物体在运动时,转动惯量可以发生变化, 是保持不变的,因此转动定律的两种表达式的意义完全一样。但在实际中,用角动量陈述的定轴转动定律适用范围更为广泛,可以适用于刚体,也可以适用于非刚体。当物体在运动时,转动惯量可以发生变化,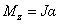 对它不再适用,但 对它不再适用,但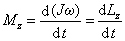 对它还是成立的。 对它还是成立的。 |