一个与外界没有相互作用的系统称为孤立系统。对孤立系统,外力的功当然为零,即 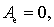 则 则
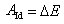
上式表明,如果系统状态变化时,有非保守内力做功,它的机械能当然就不守恒了。但大量实验证明,一个孤立系统经历任何变化过程,系统内各种形式的能量总和是不变的,能量只能从一种形式转化为另一种形式,或从系统内的一个物体传递给另一个物体。这就是能量转化和守恒定律。它是物理学中具有最大普遍性的定律之一。
若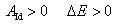 ,表明系统内机械能增加,其他形式的能量转化为机械能。 ,表明系统内机械能增加,其他形式的能量转化为机械能。
若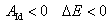 ,表明系统内机械能减少,机械能转化为其他形式的能量。 ,表明系统内机械能减少,机械能转化为其他形式的能量。
能量转化和守恒定律是自然界最基本的规律之一。一方面,自然界一切已经实现的过程无一例外遵守着这些守恒定律。如果发现有所违反,那常常因为过程中孕含着还未被认识的新事物。于是人们就按守恒定律要求去寻找和发现新事物。20世纪物理学的发展过程中有不少这样的事例。
另一方面,凡违背守恒定律的过程就是不能实现的,因此可根据守恒定律判断哪些过程不可能发生,哪些构想不可能实现。历史上曾有许多人企图发明一种“永动机”,它不消耗能量而能连续不断地对外做功,或消耗少量能量而作大量的功。这种设想违反能量守恒定律,这类永动机只能以失败而告终。此外,利用守恒定律研究物体系统,可不管系统内各物体的相互作用如何复杂,也不问过程的细节如何,而直截了当地对系统的始末状态的某些特征下结论,为解决问题另辟新路子,这也是守恒定律的特点和优点。 |