人们在生产活动和科学实践中发现,物质运动的形式是多种多样的,我们必须选用一个能够反映各种运动形式的共性的物理量,作为各种运动形式的一般量度,这个量就是能量。对应于物体的某一状态,必定有一个而且只能有一个能量值。如果物体状态发生变化,它的能量值也随之变化。因此,能量是物体状态的单值函数。物体作机械运动,它的状态是用位置和速度描述的,我们把位置和速度叫做状态参量。这样,量度机械运动的机械能应是位置和速度的单值函数。现在,我们将通过动能定理的介绍,了解机械能的一种具体表式以及它与功的关系。
当物体在变力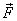 作用下,从 作用下,从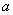 点沿曲线运动到 点沿曲线运动到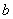 点时,我们用 点时,我们用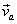 和 和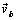 分别表示它在起点 分别表示它在起点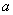 和终点 和终点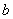 处的速度,如图所示。由功的定义,变力 处的速度,如图所示。由功的定义,变力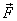 在这过程中所作的功是 在这过程中所作的功是
式中的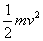 叫物体的动能,用 叫物体的动能,用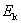 表示,即 表示,即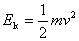
它是机械能的一种形式。因此,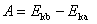
上述关系是牛顿第二定律的又一积分形式,它常被叫做动能定理。
关于动能定理的几点说明
(1)动能和功的单位是一样的,但是意义不同。
(2)由于位移和速度的相对性,功和动能也都有相对性,它们的大小都依赖于参考系的选择。
(3)动能定理中的功应理解为合外力的功,合外力所做的功等于各分力所做功的代数和。
(4)虽然动能定理由牛顿第二定律积分而来,但由于合外力对物体所作的功总是取决于物体始末动能之差,我们无需去研究物体在每一时刻的运动情况。这样,动能定理在解决某些力学问题时,往往比直接运用牛顿第二定律的瞬时关系要简便得多。
(5)动能定理的微分形式 |