高斯定理

二、高斯定理

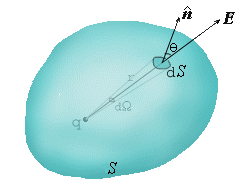考虑一个点电荷q的电场中，有一闭合曲面S，在S上取一面元dS，设r是该电荷到面元的距离，是面元的外法线单位矢量，则通过该面元的电通量： 式中θ是面元处的场强与的夹角。

应用立体角的概念：

所以：

对整个闭合曲面S，电通量为：

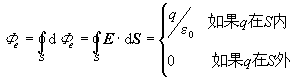
    这是对单个点电荷的高斯定理。根据场强的叠加原理，上述结果可推广至任意带电系统的静电场。对于点电荷系，高斯定理可写为：

式中只对闭合曲面S内的电荷求和。

对于连续分布电荷，高斯定理写为：

式中V是闭合曲面S所包围的体积，ρ是电荷体密度。需要说明，高斯定理指出的定量关系依赖于：

    1 电荷间作用力的平方反比律
    2 力的有心性质
    3 不同电荷效应的线性叠加

    对于牛顿引力场来说，具有与静电场相似的性质，因此只要以质量密度代替电荷密度，高斯定理在引力场中也成立。