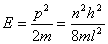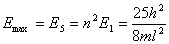 ,谱线宽度 ,谱线宽度 的光子,试估算: 的光子,试估算:(1)此光子的动量不确定度 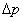 ; ;(2)此光子的位置不确定度 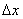 ; ;(3)原子处在激发态的寿命 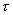 ; ;(4)该激发态的能量宽度 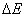 。 。 |
||
【解】(1)光子的动量 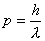 光子动量的不确定度 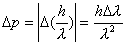 (2)由不确定关系 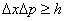 得光子位置的不确定度 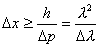 (3)原子在激发态的寿命 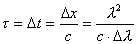 (4)激发态的能量宽度 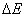 可由不确定关系 可由不确定关系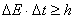 来估算得 来估算得
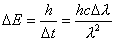 |
||
(1)德布罗意波的驻波条件; (2)不确定关系式; (3)薛定谔方程。 |
||
【解】(1)要达到稳定状态,德布罗意波在势阱中应形成驻波,能量最小时驻波的波长为2a,该势阱中粒子的动量
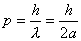 相应的能量 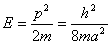 (2)由测不准关系 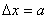 , ,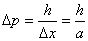 取粒子的动量p与动量的测不准量 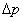 为同一数量级,即 为同一数量级,即 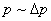 得粒子的能量 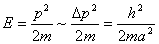 (3)根据薛定谔方程求解 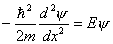 即 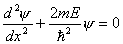 令 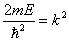 , ,原方程可写成: 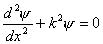 方程的解为: 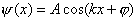 由边界条件 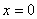 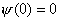 得: 得: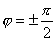 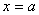 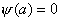 得: 得: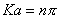 由此得 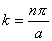 ,又因为上面已令 ,又因为上面已令 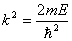 因此 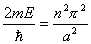 得 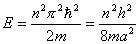 最小时 n=1 得 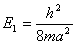
|
||
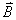 中,考虑到轨道磁矩与外磁场的相互作用,讨论该状态的能级分裂情况,并计算跃迁发出光子的频率。 中,考虑到轨道磁矩与外磁场的相互作用,讨论该状态的能级分裂情况,并计算跃迁发出光子的频率。 |
||
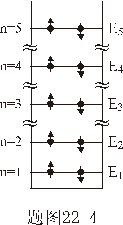
【解】氢原子处在外磁场中,由于空间量子化,电子轨道角动量相对外磁场方向有各种可能的取向,电子轨道磁矩也有相应的不同取向,导致氢原子与外磁场之间不同的相互作用势能,使氢原子电子轨道磁矩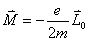 电子磁矩与外磁场相互作用能 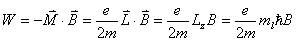 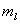 的可能取值有 的可能取值有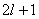 个,磁矩与外磁场相互作用能也出现 个,磁矩与外磁场相互作用能也出现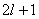 个可能值。 个可能值。对应于氢原子2p态与外磁场的相互作用能有三个不同值,分别为 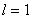 ; ;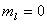 , ,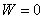 , ,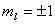 , ,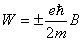 。1s能级不变化,2p能级分裂为三个能级,相邻之间能级的能量差为 。1s能级不变化,2p能级分裂为三个能级,相邻之间能级的能量差为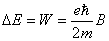 。 。原先由2p跃迁至1s的一条谱线分裂成为三条谱线,如图22-3所示。 其频率分别为: 原频率 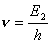 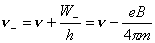 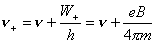 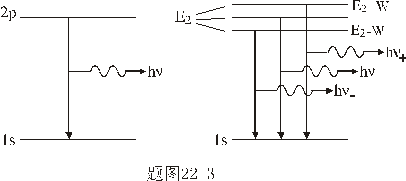 |
||
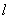 。若忽略电子间的相互作用,应用量子物理的基本原理计算系统处于最低能量时,势阱中电子的最大能量。 。若忽略电子间的相互作用,应用量子物理的基本原理计算系统处于最低能量时,势阱中电子的最大能量。 |
||
|
||
(1)画出电子在外电场中的总势能曲线; (2)试从量子力学效应定性解释电子从金属中逃逸的原因。 |
||
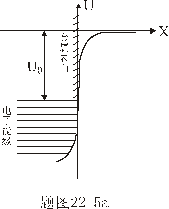 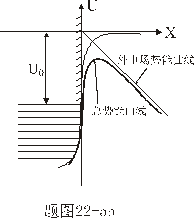 【解】(1)外加磁场沿x 负方向, 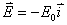 ,电子在外电场的电势能 ,电子在外电场的电势能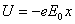 ,由此可画出电子在外电场中的势能曲线及电子在外电场中的金属表面处的总势能曲线图22-5b。 ,由此可画出电子在外电场中的势能曲线及电子在外电场中的金属表面处的总势能曲线图22-5b。(2)加上外电场后,原无限宽势能曲线变为变有限宽的势垒,根据量子力学隧道效应,电子将穿过势垒逃逸金属 |
||
【解】电子自旋磁矩 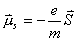 设质子产生的磁场为 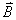 ,自旋磁矩与磁场的相互作用能 ,自旋磁矩与磁场的相互作用能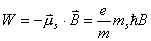 自旋方向从与 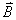 平行变为与 平行变为与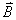 反平行, 反平行,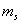 从 从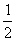 变为 变为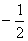 ,则能量的变化为 ,则能量的变化为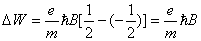 题意中表明银河系中氢原子发射的谱线波长 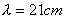 ,可知 ,可知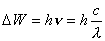
解上两式: 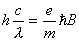 得: 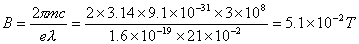 |
||
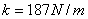 ,C和O的质量分别为 ,C和O的质量分别为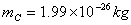 , ,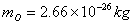 。试计算: 。试计算:(1)相对振动的频率; (2)相邻两个振动能级的间距。 |
||
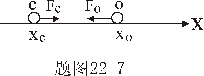 【解】(1)设CO分子中C与O原子间距为 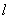 ,系统在振动过程中C、O的坐标分别为 ,系统在振动过程中C、O的坐标分别为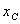 和 和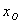 ,如图22-7所示。 ,如图22-7所示。据牛顿定律 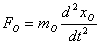 (1) (1)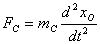 (2) (2)C和O之间的键合作用力 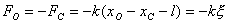 式中 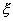 为C、O对平衡位置的相对位移。将(1)、(2)式改写成 为C、O对平衡位置的相对位移。将(1)、(2)式改写成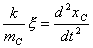 (3) (3)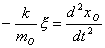 (4) (4)(4)式减(3)式改写成为: 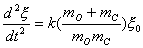 因此,谐振动圆频率 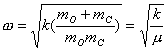 式中 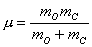 为C、O两体系统的约化质量。 为C、O两体系统的约化质量。代入已知数据,得到CO分子中两原子相对振动的频率。 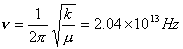 (2)根据谐振子的能量公式: 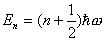 相邻两个振动能级的能量 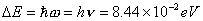 |
||
【解】二维无限深势阱的薛定谔方程为: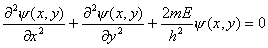 (1)
(1)设波函数 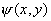 有两个独立函数 有两个独立函数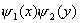 乘积组成,并将E写成为 乘积组成,并将E写成为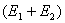 ,则(1)式可改写成 ,则(1)式可改写成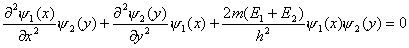 (2) (2)(2)式也可写成: 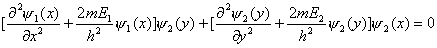 若能使 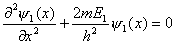 (3) (3)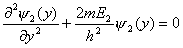 (4) (4)则可以找到 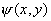 的解,由于波函数满足单值条件也就是找到了原方程(1)的解了。 的解,由于波函数满足单值条件也就是找到了原方程(1)的解了。由(3)(4)式,仿照一维无限深方势阱,我们可得: 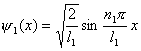 式中 式中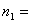 1,2,3…… 1,2,3……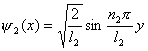 式中 式中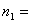 1,2,3…… 1,2,3……得:  相应还可求得能量: 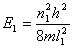 , , 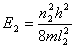 , , 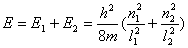 |