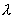 ,每缝缝宽 ,每缝缝宽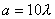 ,相邻缝间不通光部分的宽度 ,相邻缝间不通光部分的宽度 ,四缝前所用透镜的焦距 ,四缝前所用透镜的焦距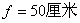 ,光屏放在焦平面上,试画出在光屏上离中央明条纹到10厘米范围内光强分布的大致情况。 ,光屏放在焦平面上,试画出在光屏上离中央明条纹到10厘米范围内光强分布的大致情况。 |
| 【解】画此光强分布图应从以下四方面考虑: 1、单缝衍射因子的影响:单缝衍射包迹暗条纹的位置满足: 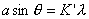 (1) (1)即: 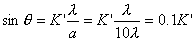 由题设 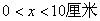 ,又 ,又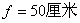 ,所以衍射角 ,所以衍射角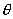 很小,所以有 很小,所以有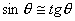 ,因此包迹暗条纹的位置: ,因此包迹暗条纹的位置: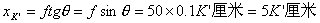 处 处即: 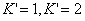 相应 相应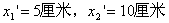 2、四缝干涉明条纹位置: 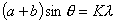 (2) (2)即: 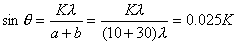 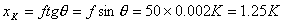 在 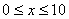 厘米范围内,取K=0,1,2,……8,相应的x为:0,1.25,2.5……10厘米。 厘米范围内,取K=0,1,2,……8,相应的x为:0,1.25,2.5……10厘米。3、 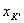 与 与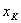 重迭处为缺级位置,(2)式比(1)式得: 重迭处为缺级位置,(2)式比(1)式得: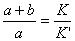 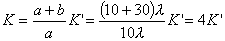 即: 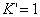 和2处;K=4和8明条纹位置为缺级。 和2处;K=4和8明条纹位置为缺级。4、四缝干涉中应有 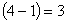 个暗纹位置,有 个暗纹位置,有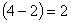 个次明位置,根据以上讨论可大致画出这单缝衍射对四缝干涉调制后的光强分布图。如图20-1所示。 个次明位置,根据以上讨论可大致画出这单缝衍射对四缝干涉调制后的光强分布图。如图20-1所示。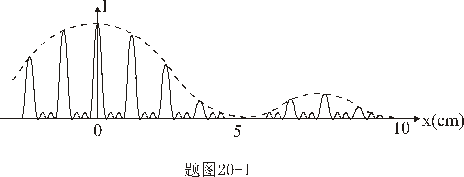 |
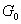 为标准块规, 为标准块规,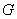 为待测上端面的块规,用波长为 为待测上端面的块规,用波长为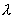 的平行光垂直照射,测得平晶与块规之间空气劈尖的干涉条纹如图所示,对于与 的平行光垂直照射,测得平晶与块规之间空气劈尖的干涉条纹如图所示,对于与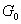 和 和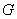 的条纹间距分别为 的条纹间距分别为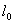 和 和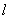 ,且 ,且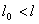 。若将 。若将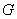 转过 转过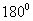 ,两侧条纹均比原来密。 ,两侧条纹均比原来密。(1)判断并在图c中画出 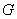 规上端面的形貌示意图; 规上端面的形貌示意图;(2)求 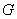 规左、右侧与 规左、右侧与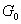 的高度差。 的高度差。 |
 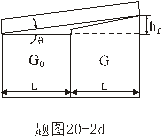 【解】(1)可以想象待测块规端面误差放大后的正视图,只有这样才满足题意。 (2)左右干涉条纹的数目分别为: 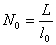 , ,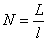 平晶与标准块规之间的夹角 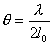 , ,可得待测块规右边比标准块规高: 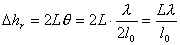 左边待测块规比标准块规高 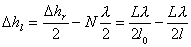 |
| |
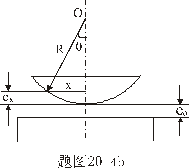
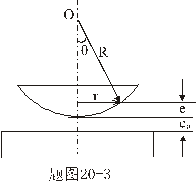 【解】设平凸透镜凸面与平面玻璃之间存在着一气隙,气隙的厚度为 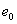 ,如图20-3所示。由于r<<R ,如图20-3所示。由于r<<R图中, 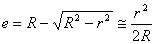 ,平凸透镜凸面和平面镜两条反射光线的总光程差 ,平凸透镜凸面和平面镜两条反射光线的总光程差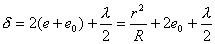 明条纹条件: 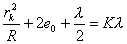 即: 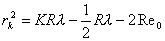 (1)
(1)得: 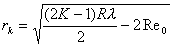 暗条纹条件: 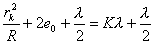 即: 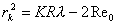 得: 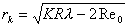 (2)
(2)对离环心较远r处各级明暗条纹间距计算方法有三: 方法一, 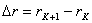 ,如直接用(2)式计算,则较烦,可采用 ,如直接用(2)式计算,则较烦,可采用 得: 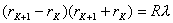 式中 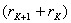 可近似看作两环平均距离r的2倍,所以上式可写成: 可近似看作两环平均距离r的2倍,所以上式可写成: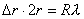 得: 得: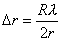 方法二,将式 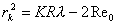 或 或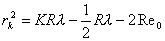 微分。由于 微分。由于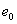 为恒量,得: 为恒量,得: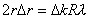 。因求某级明条纹或暗条纹间距,取 。因求某级明条纹或暗条纹间距,取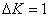 ,得 ,得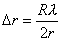 。 。方法三,在r附近极小的区域内,球面的一小部分与平面玻璃相当于劈尖的一小部分。由图不难看出,在球面r处作一切平面,与平面玻璃的夹角即为图中的 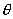 角, 角,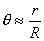 ,利用劈尖干涉条纹间距公式 ,利用劈尖干涉条纹间距公式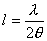 ,同样可得在r处牛顿环条纹间距 ,同样可得在r处牛顿环条纹间距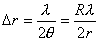 此式表示,离环心r处的条纹间距 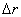 与 与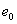 以及该处干涉级数K无关。这与平行薄膜形成的等倾干涉的圆环形干涉条纹有明显的区别,而在等倾干涉中离环心r处的干涉条纹间距 以及该处干涉级数K无关。这与平行薄膜形成的等倾干涉的圆环形干涉条纹有明显的区别,而在等倾干涉中离环心r处的干涉条纹间距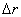 随薄膜的厚度增大或该处干涉级数K增大,条纹间距减小或条纹变密。 随薄膜的厚度增大或该处干涉级数K增大,条纹间距减小或条纹变密。
|
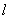 的柱面透镜一端与平板玻璃相接触,一端与平板玻璃相隔很小高度 的柱面透镜一端与平板玻璃相接触,一端与平板玻璃相隔很小高度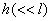 ,柱面透镜的曲率半径为 ,柱面透镜的曲率半径为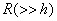 。试求: 。试求:(1)在波长为 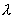 的单色光垂直照射下(z轴负方向),试判别所观测到的干涉条纹的大致形状; 的单色光垂直照射下(z轴负方向),试判别所观测到的干涉条纹的大致形状;(2)沿透镜长度方向第N个暗条纹距接触点的距离为多少? (3)沿透镜长度垂直方向第N个暗条纹距接触点的距离又为多少? |
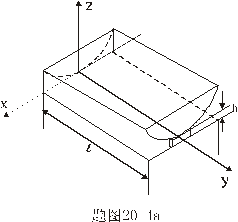  【解】(1)在 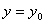 的平面,该平面与柱面透镜的截面形状如图b所示。在z方向的引起的光程差类同例20-3。 的平面,该平面与柱面透镜的截面形状如图b所示。在z方向的引起的光程差类同例20-3。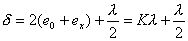 为暗条纹 为暗条纹式中 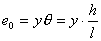 , ,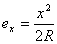 代入上式 代入上式得: 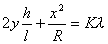 为K级暗条纹方程 为K级暗条纹方程即干涉条纹的形状为 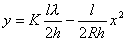 的抛物线方程。 的抛物线方程。取K为0,1,2,……形成相应的各级干涉暗条纹,如图c所示。(注:严格地说,等厚干涉的等厚处 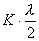 与柱面相交应形成椭圆方程。由于本题中的干涉条纹只是椭圆方程中的极小一部分,所以如上数学处理,近似为抛物线方程) 与柱面相交应形成椭圆方程。由于本题中的干涉条纹只是椭圆方程中的极小一部分,所以如上数学处理,近似为抛物线方程)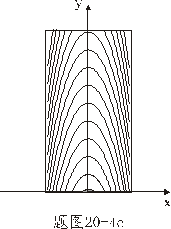 (2)沿y方向相当于劈尖干涉。 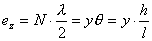 得: 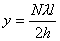 (3)沿x方向相当于牛顿环的干涉条纹在抛物线方程 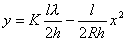 中, 中,令y=0,并将K换写成N,得 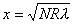
|
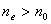 , ,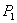 、 、 的偏振化方向相互正交,与光轴方向皆成 的偏振化方向相互正交,与光轴方向皆成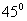 角。若以波长为 角。若以波长为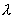 的单色自然光垂直照射,试讨论: 的单色自然光垂直照射,试讨论:(1)通过晶片C不同厚度处出射光的偏振态; (2)经过偏振片  的出射光干涉相长及相消位置与劈尖厚度d之间的关系,并求干涉相长的光强与入射光光强之比; 的出射光干涉相长及相消位置与劈尖厚度d之间的关系,并求干涉相长的光强与入射光光强之比;(3)若转动  到与 到与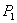 平行时,干涉条纹如何变化?为什么? 平行时,干涉条纹如何变化?为什么?(4)若改用白色自然光照射,干涉条纹又将作何变化? |
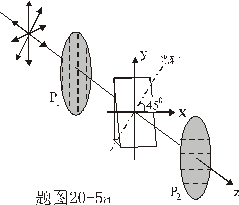 【解】请先回顾例19-2。 (1)当晶片厚度满足 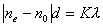 时,即 时,即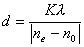 处,为全波片。经过该处的出射光为振动方向与 处,为全波片。经过该处的出射光为振动方向与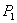 偏振化方向相同的偏振光。 偏振化方向相同的偏振光。当晶片厚度满足 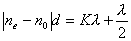 时(K=0, 时(K=0,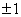 ,……),即 ,……),即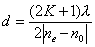 处为半波片,经过该处的出射光振动方向与 处为半波片,经过该处的出射光振动方向与 偏振化方向相同的偏振化方向相同的偏振光。 偏振化方向相同的偏振化方向相同的偏振光。当晶片厚度满足 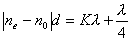 时,即 时,即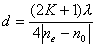 处,为 处,为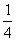 或 或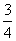 波片。经过C后的出射光线为圆偏振光。 波片。经过C后的出射光线为圆偏振光。晶片厚度不满足上述情况的,经过C后的出射光线均为椭圆偏振光。 (2)经过  的两相干光的光程差 的两相干光的光程差 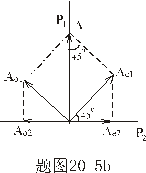 即: 即: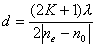 ,相当于半波片时为相长干涉。设自然光 ,相当于半波片时为相长干涉。设自然光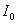 经过 经过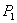 后的光振幅为A,由图20-5b可知经过 后的光振幅为A,由图20-5b可知经过 后的光振幅 后的光振幅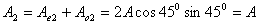 ,所以经过 ,所以经过 的偏振光与通过 的偏振光与通过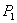 的偏振光强相同,也为 的偏振光强相同,也为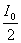 。 。当经过  的两相干光的光程差 的两相干光的光程差 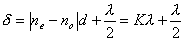 即: 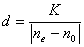 (相当于全波片时)干涉相消,出射光强为零。 (相当于全波片时)干涉相消,出射光强为零。(3)转动  到与 到与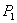 平行时,经过晶片C的o光与e光的光振动在 平行时,经过晶片C的o光与e光的光振动在 上的投影不再有 上的投影不再有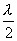 附加光程差,因为与(2)中的相长与相消干涉条纹为互换。 附加光程差,因为与(2)中的相长与相消干涉条纹为互换。(4)用白光照射时,各种波长相应的半波片与全波片相应的厚度就在不同的位置。因为出现与晶片棱边相平行的彩色干涉条纹。 |
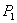 和 和 之间插入一 之间插入一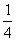 波片,波片的光轴与 波片,波片的光轴与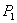 的偏振化方向间成 的偏振化方向间成 角,入射的单色自然光光强为 角,入射的单色自然光光强为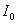 。若旋转 。若旋转 ,试计算经过 ,试计算经过 的最大光强,最小光强以及 的最大光强,最小光强以及 平行于 平行于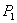 偏振化方向时的光强。 偏振化方向时的光强。 |
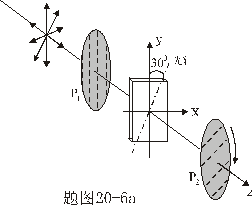  【解】本题通过偏振光干涉所作的光强计算给出了椭圆偏振光经偏振片后干涉叠加的过程。 自然光经 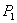 偏振片后成为线偏振光,其光强为 偏振片后成为线偏振光,其光强为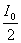 。线偏振光在 。线偏振光在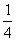 波片C中分成o光和e光,经过波片后的位相差为 波片C中分成o光和e光,经过波片后的位相差为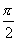 ,振幅分别为(见图b)。 ,振幅分别为(见图b)。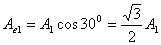 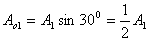 经过 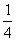 波片后为椭圆偏振光,其长轴沿波片的光轴方向,短轴垂直于光轴。 波片后为椭圆偏振光,其长轴沿波片的光轴方向,短轴垂直于光轴。转动偏振片  ,当其偏振化方向与光轴平行时,经过 ,当其偏振化方向与光轴平行时,经过 的光强最大: 的光强最大: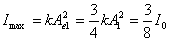 当  的偏振化方向转到与光轴垂直时,经过 的偏振化方向转到与光轴垂直时,经过 的光强最小: 的光强最小: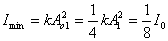 当  的偏振化方向转到与 的偏振化方向转到与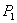 偏振化方向平行时,经过 偏振化方向平行时,经过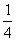 波片的两束光在 波片的两束光在 偏振化方向的分量为(见图b) 偏振化方向的分量为(见图b)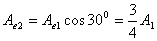 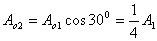 两光的位相差为 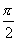 ,经过偏振片 ,经过偏振片 后的干涉光强为: 后的干涉光强为: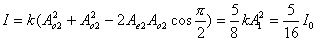
|
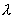 的单色光照在各缝相邻间距为d的三缝上,设每缝的缝宽都很窄,在衍射角 的单色光照在各缝相邻间距为d的三缝上,设每缝的缝宽都很窄,在衍射角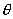 较小的范围内忽略单缝衍射因子的影响。 较小的范围内忽略单缝衍射因子的影响。试证明三缝干涉的光强分布为: 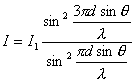 |
【证明】相邻缝间在衍射角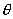 方向上光波的光程差如图20-7a所示。 方向上光波的光程差如图20-7a所示。 相应的相位差 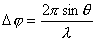 设各缝光矢量的振幅为 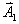 、 、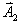 、 、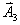 ,它们的大小都相等为 ,它们的大小都相等为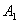 ,三缝三光矢量合成图如图b所示。合振幅 ,三缝三光矢量合成图如图b所示。合振幅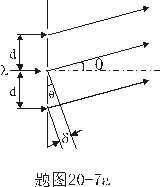 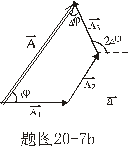 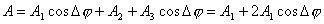 或 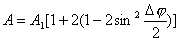 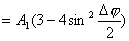 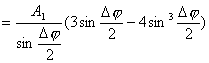 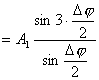 三缝干涉的光强分布 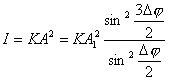 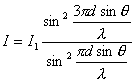 得证。 得证。三缝干涉的光强分布如图c所示。  为便于理解光强分布图的意义,我们将光强分布图上的①②③④位置处的三缝各光矢量 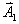 、 、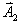 、 、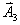 的合成情况画在图d中,可知: 的合成情况画在图d中,可知:干涉主极大位置满足 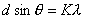 干涉极小位置满足 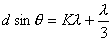 和 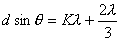 |
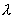 。若在三缝装置的中缝前贴上光程差为 。若在三缝装置的中缝前贴上光程差为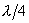 的薄膜,在透镜焦平面上光强如何分布?并大致画出光强分别曲线。 的薄膜,在透镜焦平面上光强如何分布?并大致画出光强分别曲线。 |
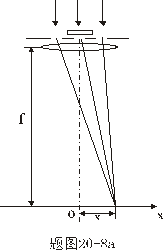 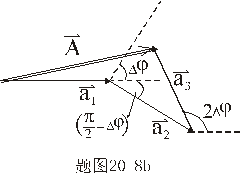 【解】衍射角为 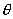 时,相邻两缝出射光的光程差 时,相邻两缝出射光的光程差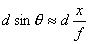 相邻光线的位相差 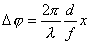 1、2两缝光线的位相差为 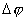 ,1、3两缝光线的位相差为 ,1、3两缝光线的位相差为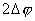 。设各缝出射光的光振幅 。设各缝出射光的光振幅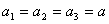 ,中缝未加薄膜时光振幅矢量合成如上例图20-7b所示。在中缝前加上薄膜,在同一衍射角 ,中缝未加薄膜时光振幅矢量合成如上例图20-7b所示。在中缝前加上薄膜,在同一衍射角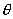 的情况下,相邻缝的出射光之间的位相差改变,1、2缝出射光的位相差为 的情况下,相邻缝的出射光之间的位相差改变,1、2缝出射光的位相差为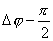 ,1、3缝出射光的位相差未受影响,仍为 ,1、3缝出射光的位相差未受影响,仍为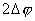 ,它的光矢量图如20-8b所示。从光振幅矢量合成图上可求得图a中P点合成光的振幅 ,它的光矢量图如20-8b所示。从光振幅矢量合成图上可求得图a中P点合成光的振幅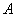 : :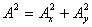 即: 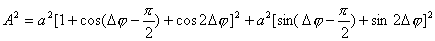 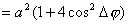 光强分布函数  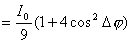 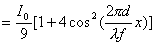 当 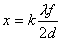 , ,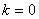 ,1,2,……时, ,1,2,……时,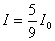 ,为干涉极大; ,为干涉极大;当 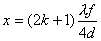 , ,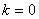 ,1,2,……时, ,1,2,……时,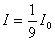 ,为干涉极小。 ,为干涉极小。光强分布曲线如图20-8c所示。 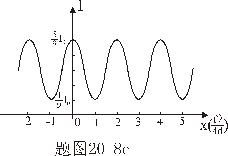 |
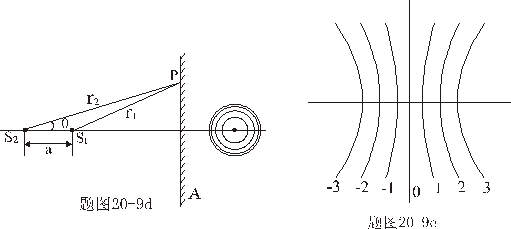
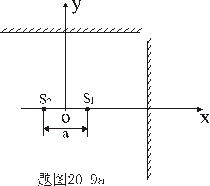
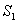 、 、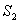 两球面波相干光源,相距很近,间距为a,如图20-9a所示。 两球面波相干光源,相距很近,间距为a,如图20-9a所示。(1)试讨论两相干光源的干涉场,并画出空间光强分布; (2)分别画出垂直于x轴的光屏A和垂直于y轴的光屏B上的明条纹分布。 |
|
| 【证明】第一步,用相对论效应导出光的多普勒效应。 设光源以速度 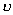 相对于观察者运动。见图20-10a可得光对观察者的波长为: 相对于观察者运动。见图20-10a可得光对观察者的波长为: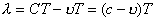 式中T为光源发射一个波长所用的时间。由于光源相对于观察者在运动。相对于观察者运动的钟变慢。 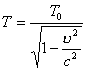 代入上式: 代入上式: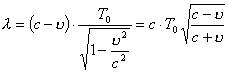 可改写成: 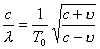 也就是: 也就是: 式中 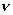 为观察者所测得的频率, 为观察者所测得的频率, 是相对于光源静止坐标系内的光源发射的光波的频率。 是相对于光源静止坐标系内的光源发射的光波的频率。在光源相对于观察者运动的速度不太大时( 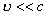 ) )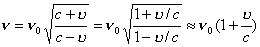 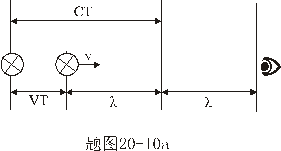 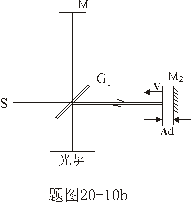 第二步,用光的多普勒效应公式导出迈克耳逊干涉仪中的条纹移动公式。 见图20-10b所示的迈克耳逊干涉仪。固定镜 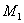 反射光照到光屏处的光屏仍为光源S的光频 反射光照到光屏处的光屏仍为光源S的光频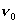 而反射镜 而反射镜 在相对于光源S运动时, 在相对于光源S运动时, 接收到光频。由光的多普勒效应公式 接收到光频。由光的多普勒效应公式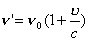 由于  在以速度 在以速度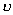 运动,作为反射光的光源,再一次应用多普勒效应公式,反射光的频率 运动,作为反射光的光源,再一次应用多普勒效应公式,反射光的频率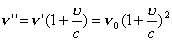 因为 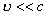 所以光屏接收到 所以光屏接收到 反射的光频可近似表示为 反射的光频可近似表示为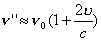 这一光频与反射镜 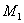 照射到光屏上的光频 照射到光屏上的光频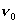 产生拍频 产生拍频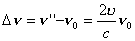 式中 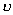 为 为 运动的距离 运动的距离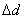 和时间 和时间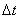 的比值即 的比值即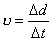 代入上式: 代入上式: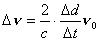 由此得: 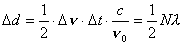 式中 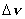 为光强在屏上每秒钟改变的次数, 为光强在屏上每秒钟改变的次数,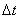 是 是 在运动 在运动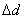 中所用的时间。所以在此过程中光屏上光强的变化次数即干涉条纹变化的次数 中所用的时间。所以在此过程中光屏上光强的变化次数即干涉条纹变化的次数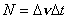 。这样本题得到了证明。 。这样本题得到了证明。 |
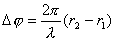
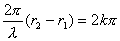 或
或
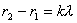
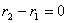 时,零级干涉极大为
时,零级干涉极大为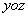 平面;
平面;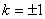 ,
,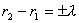 ,一级干涉极大为以x为轴的旋转双曲面;
,一级干涉极大为以x为轴的旋转双曲面;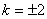 ,
,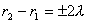 ,二级干涉极大为旋转双曲面。空间光强极大区域是一系列绕x轴旋转的双曲面,如图20-9c所示。
,二级干涉极大为旋转双曲面。空间光强极大区域是一系列绕x轴旋转的双曲面,如图20-9c所示。
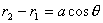 ,光程差由倾角
,光程差由倾角