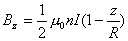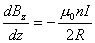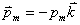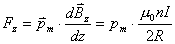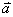 ,若导体内的电流密度均匀为 ,若导体内的电流密度均匀为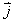 , ,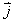 的方向平行与轴线。求腔内任意点的磁感应强度 的方向平行与轴线。求腔内任意点的磁感应强度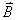 。 。 |
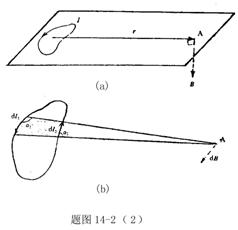
  【解】半径为R的无限长圆柱形直线电流在柱体内离轴线r处的磁感应强度 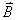 可根据安培环路定理: 可根据安培环路定理: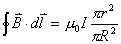 即: 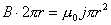 得: 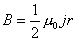 写成矢量形式: 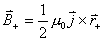 现在在这圆柱形导线内有一空腔,则和原实心圆柱体内在该圆柱形空腔处有一反向电流, 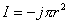 迭加是等效的,反向电流在空腔处产生的磁感应强度: 迭加是等效的,反向电流在空腔处产生的磁感应强度: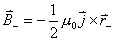 由迭加原理,腔内的磁感应强度 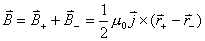 由导线的横截面图b,可得: 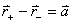 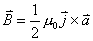 此式表明空腔内是一均匀磁场,它的大小 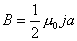 ,它的方向垂直于 ,它的方向垂直于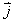 ,亦垂直于 ,亦垂直于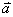 。 。 |
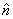 ,它的磁矩 ,它的磁矩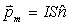 ,求证在离线圈中心远大于线圈线度的r处的磁感应强度,即磁偶极子的磁感应强度 ,求证在离线圈中心远大于线圈线度的r处的磁感应强度,即磁偶极子的磁感应强度 。 。 |
【证明】第一步先求如图14-2a所示在线圈轴线方向上,离线圈中心
|
| |
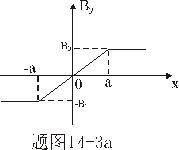 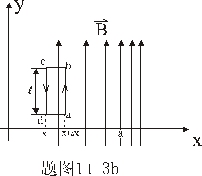 【解】题图的磁感应图线的函数式 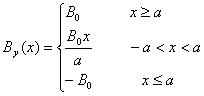 在xy平面上某一区域的磁感应线如图分布。并在xy平面内作一闭合回路 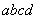 。由安培环路定理 。由安培环路定理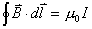 即 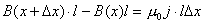 式中 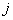 为回路所包围的小区域内沿z方向的传导电流密度的平均值,当 为回路所包围的小区域内沿z方向的传导电流密度的平均值,当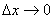 时,即得x处的传导电流密度的准确值,即: 时,即得x处的传导电流密度的准确值,即: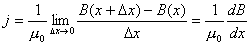 所以,在 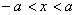 区域内 区域内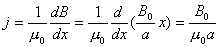 在 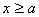 和 和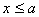 区域 区域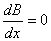 ,即无传导电流也就是 ,即无传导电流也就是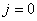 。 。
|
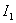 为垂直于纸面无限长导线中的电流, 为垂直于纸面无限长导线中的电流,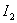 为纸面内一段导线中的电流,a为纸面内一段导线的长度,b为两导线间垂直距离。求通有 为纸面内一段导线中的电流,a为纸面内一段导线的长度,b为两导线间垂直距离。求通有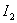 导线所受的力。 导线所受的力。 |
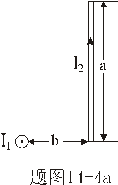 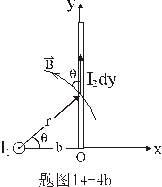 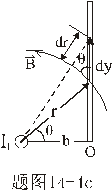 【解】由安培定律有限长导线2上电流元 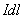 所受的安培力的大小 所受的安培力的大小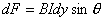 由图b可以判别导线2上各电流元所受安培力的方向都是垂直纸面向外,式中B为无限长直导线电流 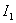 所产生的磁场,由此上式可改写成: 所产生的磁场,由此上式可改写成:
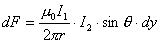 由图b,上式中 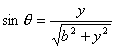 ,所以 ,所以 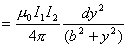 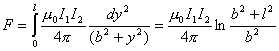 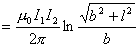 本题也可由图c的几何关系进行变量替换: 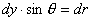 由此 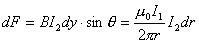 积分得: 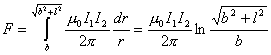 方向垂直纸面向外 方向垂直纸面向外 |
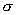 ,当圆柱面绕其轴线以匀角速 ,当圆柱面绕其轴线以匀角速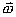 旋转,如图14-5a所示,求圆柱表面单位面积上所受的磁场力。 旋转,如图14-5a所示,求圆柱表面单位面积上所受的磁场力。 |
|
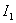 的导线平面内,有一扇形线框,通电为 的导线平面内,有一扇形线框,通电为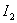 尺寸位置如图14-6a所示。求这扇形线框所受的磁力矩。 尺寸位置如图14-6a所示。求这扇形线框所受的磁力矩。 |
【解】方法一,扇形线框的两弧线与电流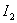 产生的磁力线方向平行,所以不受力。而径向导线ab和cd垂直与磁力线所受的安培力大小相等,方向相反,对对称轴x轴产生磁力矩。在导线ab一电流元对x轴的磁力矩(参阅图a) 产生的磁力线方向平行,所以不受力。而径向导线ab和cd垂直与磁力线所受的安培力大小相等,方向相反,对对称轴x轴产生磁力矩。在导线ab一电流元对x轴的磁力矩(参阅图a)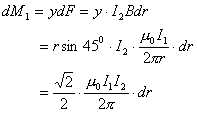 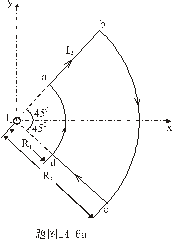 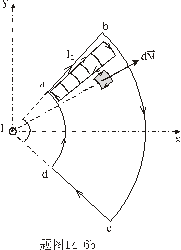 ab,cd两导线产生的磁力矩 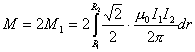 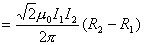 方法二,因为在线框内 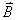 不均匀,线框所受的磁力矩不能之间用 不均匀,线框所受的磁力矩不能之间用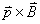 来求,但可将线圈如图14-6b分解成许多小扇形线框,小线框之间相邻的电流恰好抵消,小线框与大扇形线框相邻处电流一致。所以各小线框所受磁力矩的矢量和就是大扇形线框所受的磁力矩。其中任一小线框在磁感应强度为 来求,但可将线圈如图14-6b分解成许多小扇形线框,小线框之间相邻的电流恰好抵消,小线框与大扇形线框相邻处电流一致。所以各小线框所受磁力矩的矢量和就是大扇形线框所受的磁力矩。其中任一小线框在磁感应强度为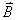 的磁场中所受的磁力矩 的磁场中所受的磁力矩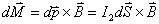 注意到  是矢量,方向如图b所示。由对称性合力矩的方向沿着x轴,所以有 是矢量,方向如图b所示。由对称性合力矩的方向沿着x轴,所以有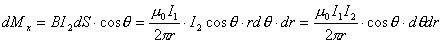 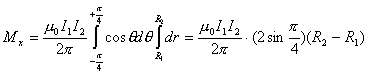 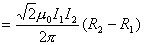 比较这两种解法可知,在非均匀磁场内用 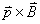 的方法仍然是正确的,特别要注意它的矢量性,否则容易出错,有时还是用电流元的安培力产生的磁力矩直接处理比较方便。 的方法仍然是正确的,特别要注意它的矢量性,否则容易出错,有时还是用电流元的安培力产生的磁力矩直接处理比较方便。 |
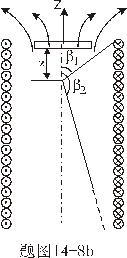
 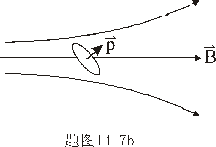 【解】磁偶极子在非均匀磁场某一位置的磁通量 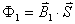 设磁偶极子在非均匀磁场内在磁场力作用下平移了dx一段距离,在新位置处的磁通量 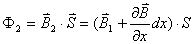 在移动过程中磁力 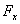 的功 的功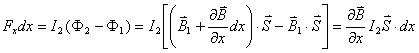 即 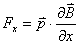 式中 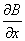 对图14-8a而言为负值,即指向x负方向。一般说来磁矩为 对图14-8a而言为负值,即指向x负方向。一般说来磁矩为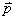 的磁偶极子处在图14-8b的非均匀磁场中,它受到的磁力矩,使 的磁偶极子处在图14-8b的非均匀磁场中,它受到的磁力矩,使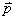 的方向要转向外磁场,又有上式可知它受的磁场力是磁感应强度的梯度方向,即指向强磁场方向。所以在非均匀磁场内的线圈在磁力矩和磁力的作用下都力图使线圈中的磁通量变大。 的方向要转向外磁场,又有上式可知它受的磁场力是磁感应强度的梯度方向,即指向强磁场方向。所以在非均匀磁场内的线圈在磁力矩和磁力的作用下都力图使线圈中的磁通量变大。 |
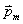 垂直向下,试求小线圈受到的磁场力。 垂直向下,试求小线圈受到的磁场力。 |
|
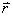 处A点的磁感应强度B。由毕奥-萨伐尔定律可知,线圈上电流元
处A点的磁感应强度B。由毕奥-萨伐尔定律可知,线圈上电流元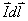 在离它
在离它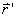 处的磁感应强度
处的磁感应强度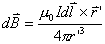
 放大、
放大、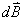 的方向垂直于
的方向垂直于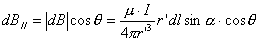
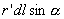 为
为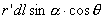 表示以A为顶点
表示以A为顶点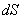 的2倍,因此上式可写成
的2倍,因此上式可写成
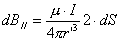
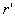 非常接近于r,上式积分中
非常接近于r,上式积分中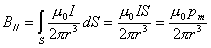
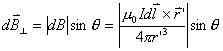
 非常接近1,
非常接近1,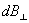 近似表示为如下矢量形式
近似表示为如下矢量形式
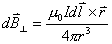
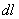 沿闭合回路积分,由于r为恒量,所以
沿闭合回路积分,由于r为恒量,所以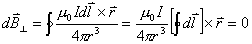
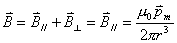
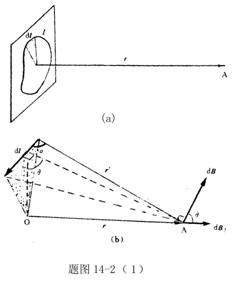
 所产生的
所产生的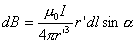 。为分析其几何关系,将
。为分析其几何关系,将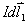 和
和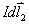 ,这两电流元在场点A处产生的磁感应强度大小分别为:
,这两电流元在场点A处产生的磁感应强度大小分别为: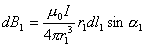
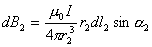
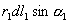 和
和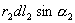 分别表示由
分别表示由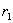 和
和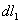 及
及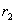 和
和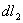 所组成的平行四边形面积
所组成的平行四边形面积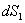 和
和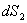 。由图2(b)可以判别,这两电流元在A处产生的磁感应强度方向相反,这两电流元产生的总磁感应强度
。由图2(b)可以判别,这两电流元在A处产生的磁感应强度方向相反,这两电流元产生的总磁感应强度
 ,且A点想线圈所引的两条割线几乎平行,所以上式可近似表示为:
,且A点想线圈所引的两条割线几乎平行,所以上式可近似表示为: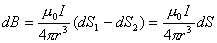
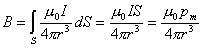
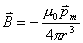
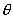 的
的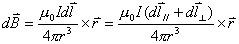
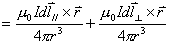
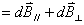
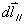 和
和 是线圈上电流元
是线圈上电流元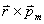 所组成的平面上的投影。这相当于将磁偶极子
所组成的平面上的投影。这相当于将磁偶极子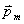 分解成
分解成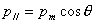 ,
,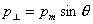 ,参照第一步和第二步结论,再判别方向后可得
,参照第一步和第二步结论,再判别方向后可得
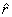 为径向单位矢量,
为径向单位矢量,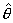 为横向单位矢量。
为横向单位矢量。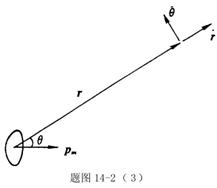
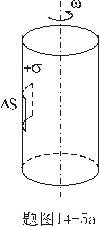

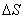 ,面积上的运动电荷
,面积上的运动电荷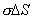 ,在其表面两侧极靠近的磁感应强度
,在其表面两侧极靠近的磁感应强度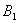 和
和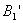 。
。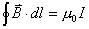
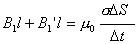
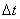 时间内运动电荷穿过yz平面的距离为
时间内运动电荷穿过yz平面的距离为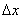 ,则上式可写成
,则上式可写成
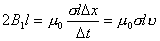
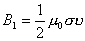
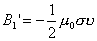
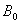 。不难理解。细长均匀带电圆柱面以匀速
。不难理解。细长均匀带电圆柱面以匀速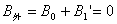
 得:
得:
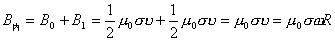
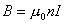 相吻合因为,对面密度为
相吻合因为,对面密度为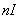 相当于
相当于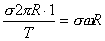 。
。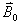 对
对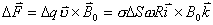
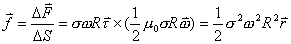

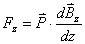 ,由此可知应先计算螺线管中心轴线上一点的磁感应强度
,由此可知应先计算螺线管中心轴线上一点的磁感应强度
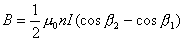 。
。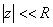 ,则
,则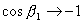 ,
,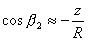 。端面近中心处的磁感应强度轴向分量
。端面近中心处的磁感应强度轴向分量