 13.3 在相对介电常数为 13.3 在相对介电常数为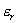 的无限大均匀介质中有一带电量为 的无限大均匀介质中有一带电量为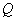 的导体 的导体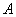 ,介质与导体界面处的极化电荷为 ,介质与导体界面处的极化电荷为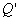 ,如图所示。试计算 ,如图所示。试计算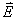 、 、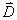 、 、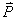 三个矢量沿封闭曲面 三个矢量沿封闭曲面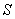 的通量。 的通量。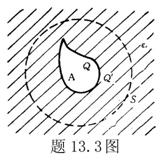  13.4 在平行板电容器中间插入一均匀电介质平板,尺寸如图a所示。现使电容器带电,试在图b、c、d、e中分别画出 13.4 在平行板电容器中间插入一均匀电介质平板,尺寸如图a所示。现使电容器带电,试在图b、c、d、e中分别画出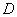 、 、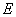 、 、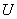 、 、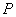 在整个电场空间中的大致分布曲线。 在整个电场空间中的大致分布曲线。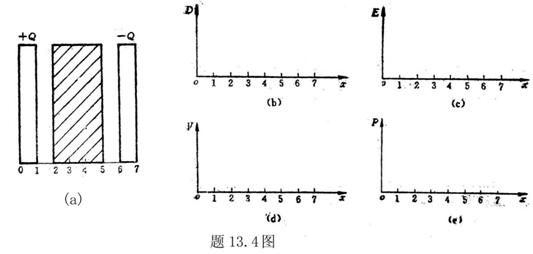  13.5 电位移矢量垂直穿过如图 13.5 电位移矢量垂直穿过如图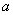 放置的无限大均匀介质平板,方向向右,分布均匀,量值为 放置的无限大均匀介质平板,方向向右,分布均匀,量值为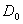 。两介质板的介电常数分别为 。两介质板的介电常数分别为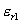 和 和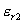 ( (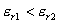 ), ),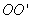 为介质分界面。 为介质分界面。(1)在图 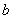 、 、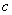 中分别画出 中分别画出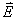 线和 线和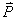 线的大致分布;(2)计算介质分界面上总的极化电荷面密度。 线的大致分布;(2)计算介质分界面上总的极化电荷面密度。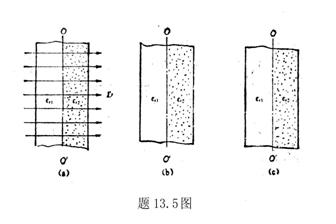  13.6 半径为 13.6 半径为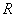 的导体球带有电荷 的导体球带有电荷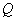 ,球外有均匀电介质同心球壳,其内外半径分别为 ,球外有均匀电介质同心球壳,其内外半径分别为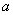 和 和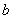 ,相对介电常数为 ,相对介电常数为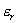 ,如图所示。试求: ,如图所示。试求:(1)介质内外的电场强度 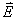 和电位移矢量 和电位移矢量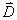 ; ;(2)介质内的极化强度 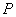 和表面上的极化电荷面密度 和表面上的极化电荷面密度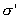 ; ;(3)介质内的极化电荷体密度 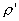 。 。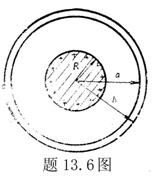 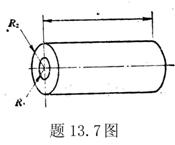  13.7 一圆柱体电容器,由半径为 13.7 一圆柱体电容器,由半径为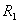 的导线和与它同轴的导体圆筒构成,圆筒半径为 的导线和与它同轴的导体圆筒构成,圆筒半径为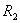 ,长为 ,长为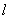 ,其间充满了相对介电常数为 ,其间充满了相对介电常数为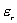 的介质,如图所示。设沿轴线单位长度上导线的电荷为 的介质,如图所示。设沿轴线单位长度上导线的电荷为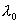 ,圆筒上单位长度的电荷为 ,圆筒上单位长度的电荷为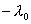 ,忽略边缘效应。试求: ,忽略边缘效应。试求:(1)介质中的电场强度 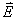 、电位移矢量 、电位移矢量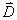 和极化强度 和极化强度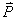 ; ;(2)介质表面的极化电荷面密度 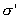 。 。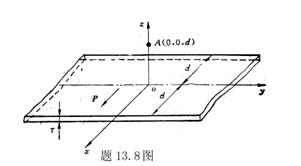  13.8 驻极体是一种特殊的电介质,它具有把极化冻结的特性,当驻极体极化后撤去外场,仍保留永久的极化强度。设有一驻极体制成的无限长薄平板,宽度为 13.8 驻极体是一种特殊的电介质,它具有把极化冻结的特性,当驻极体极化后撤去外场,仍保留永久的极化强度。设有一驻极体制成的无限长薄平板,宽度为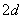 ,厚度为 ,厚度为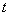 ( (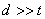 ),其均匀永久极化强度 ),其均匀永久极化强度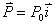 , ,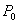 为恒量。 为恒量。(1)在图中标出驻极体的极化电荷分布; (2)求极化电荷在 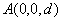 点的场强; 点的场强;(3)求 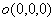 点处的电位移矢量 点处的电位移矢量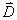 。 。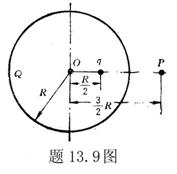 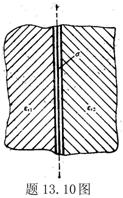  13.9 一均匀带电的薄球壳,半径为 13.9 一均匀带电的薄球壳,半径为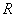 ,带电量为 ,带电量为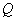 。若在壳内距中心 。若在壳内距中心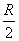 处放置一电量为 处放置一电量为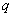 的点电荷。 的点电荷。(1)试求下列两种情况下距中心 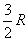 处 处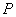 点的场强; 点的场强;(a)金属薄球壳,(b)介质薄球壳; (2)两种情况是否都可以用高斯定理求得 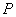 点处的场强,为什么? 点处的场强,为什么? 13.10 一无限大带电平面,电荷面密度为 13.10 一无限大带电平面,电荷面密度为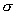 ,左、右两侧分别充满相对介电常数为 ,左、右两侧分别充满相对介电常数为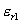 和 和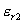 的均匀介质。 的均匀介质。(1)试问两侧介质中 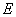 值相等还是 值相等还是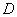 值相等,为什么? 值相等,为什么?(2)分别计算两侧介质中的电位移矢量以及介质表面的极化电荷面密度。  13.11 均匀带电、半径为 13.11 均匀带电、半径为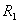 的导体球外充有两种均匀介质,相对介电常数分别为 的导体球外充有两种均匀介质,相对介电常数分别为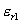 和 和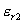 ,介质分界面半径为 ,介质分界面半径为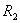 ,如图 ,如图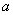 所示。 所示。(1)图 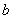 为空间电势随 为空间电势随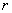 变化曲线 变化曲线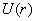 ,试画出对应的空间电场随 ,试画出对应的空间电场随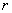 变化曲线 变化曲线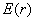 ; ;(2)试从图 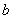 中判断是 中判断是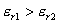 ,还是 ,还是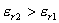 ,判据是什么? ,判据是什么?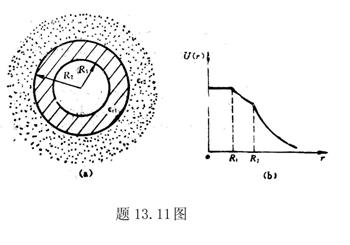  13.12 球形电容器的内外半径分别为 13.12 球形电容器的内外半径分别为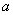 和 和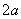 ,带电量为 ,带电量为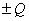 ,如图所示。电容器下半部分充有油,它的相对介电常数为 ,如图所示。电容器下半部分充有油,它的相对介电常数为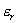 。 。(1)球面 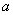 上的自由电荷和极化电荷分布是否均匀,为什么? 上的自由电荷和极化电荷分布是否均匀,为什么?(2)试求介质中任一点处的电场强度 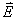 和电位移矢量 和电位移矢量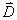 。 。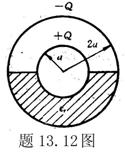
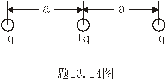  13.14 图示为三个点电荷的系统,试计算该电荷系统的相互作用能。 13.14 图示为三个点电荷的系统,试计算该电荷系统的相互作用能。 13.15 13.15 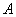 、 、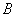 为两个同心放置的均匀带电球壳, 为两个同心放置的均匀带电球壳,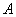 球的半径为 球的半径为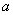 ,带电量为 ,带电量为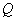 ; ;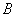 球的半径为 球的半径为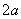 ,带电量为 ,带电量为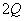 。试求: 。试求:(1) 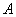 、 、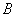 两球上电荷之间的相互作用能; 两球上电荷之间的相互作用能;(2)整个系统的静电能。 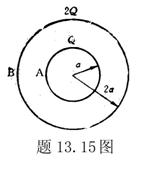  13.17 真空中半径为 13.17 真空中半径为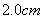 的导体球,外套有同心的导体球壳,壳的内外半径分别为 的导体球,外套有同心的导体球壳,壳的内外半径分别为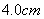 和 和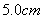 ,内球带 ,内球带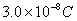 的电量。试求下列两种情况下,系统静电能的损失: 的电量。试求下列两种情况下,系统静电能的损失:(1)将导体球壳接地; (2)将导体球壳与导体球用导线相连。  13.18 两个相同的空气电容器,电容皆为 13.18 两个相同的空气电容器,电容皆为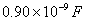 ,各自充电到电压为 ,各自充电到电压为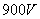 后断开电源,把其中之一浸入煤油( 后断开电源,把其中之一浸入煤油(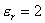 ),然后把两个电容器并联,求: ),然后把两个电容器并联,求:(1)浸入煤油过程中损失的电场能; (2)并联过程中损失的电场能。  13.19 两个同轴的长直圆柱,半径分别为 13.19 两个同轴的长直圆柱,半径分别为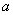 和 和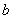 ,长为 ,长为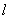 ,带有等值异号电荷 ,带有等值异号电荷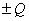 ,两圆柱之间充满介电常数为 ,两圆柱之间充满介电常数为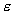 的电介质。 的电介质。(1)圆柱壳中距中心轴半径为 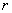 的任一点处的能量密度是多少? 的任一点处的能量密度是多少?(2)电介质中的总能量是多少? (3)试从电介质中的总能量求圆柱形电容器的电容。  13.20 如图所示, 13.20 如图所示,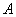 、 、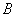 、 、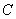 为同轴放置的三个导体柱面,半径分别为 为同轴放置的三个导体柱面,半径分别为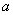 、 、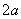 、 、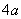 ,长为 ,长为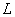 ( (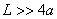 ),导体 ),导体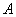 与 与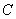 均接地,导体 均接地,导体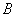 带有正电荷,其单位长度上的电量为 带有正电荷,其单位长度上的电量为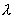 导体 导体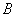 与 与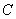 之间充满相对介电常数为 之间充满相对介电常数为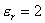 的电介质。试求: 的电介质。试求:(1)导体 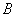 的电势; 的电势;(2) 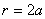 处的电极化强度; 处的电极化强度;(3)带电系统的总能量。 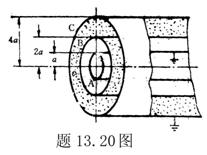 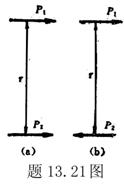  13.21 两个电偶极子中心相距为 13.21 两个电偶极子中心相距为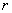 ,电偶极矩分别为 ,电偶极矩分别为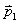 和 和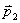 。计算下列两种情况下,两电偶极子的相互作用能: 。计算下列两种情况下,两电偶极子的相互作用能:(1)相互平行放置,如图 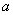 所示; 所示;(2)相互反平行放置,如图 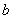 所示。 所示。 |