(1)金属板A带电 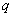 时,B板不带电求两板间的电势差 时,B板不带电求两板间的电势差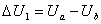 。 。(2)金属板A带电 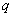 ,金属板B带电3 ,金属板B带电3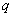 时,求两板间的电势差 时,求两板间的电势差 。 。(3)金属板A带电 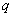 ,金属板B接地,求两板间的电势差 ,金属板B接地,求两板间的电势差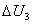 。 。 |
  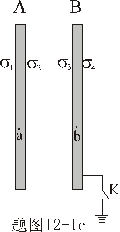 【解】(1) 我们先求A、B两板各个面上的电荷分布 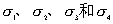 。 。在图b中,由于B板原来不带电所以有 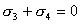 或 或 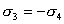 也就是由于B板。感应电荷对板外的合场强为零,所以A板的电荷分布不受B板的影响,因此得 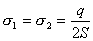 AB板间的电势差 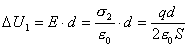 (2)给B板带电量3 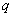 时,我们重新求解AB各表面电荷面密度 时,我们重新求解AB各表面电荷面密度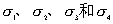 。由电荷守恒定律 。由电荷守恒定律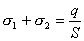 (1) (1)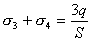 (2) (2)我们取水平向右为场强的正方向,由场板迭加原理板A内的a点和板B内的b点的合场强为零即 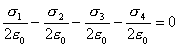 (3) (3)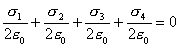 (4) (4)解以上四式得 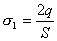 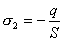 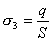 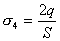 由场强迭加原理可得两板间的场强 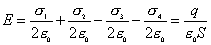 亦可用高斯定理(如图b所示);或直接用金属表面附近的场强公式  由此得AB板间电势差 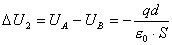 (3)将B金属板接地,应注意B板接地并非B板不带电。而是指B板的电势为零。B板的电势为零,则 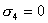 ;如果 ;如果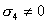 ,则根据高斯定理必有电力线由B外侧穿出到无穷远处或到地。这样B板的电势不为零与B板接地相矛盾,因此 ,则根据高斯定理必有电力线由B外侧穿出到无穷远处或到地。这样B板的电势不为零与B板接地相矛盾,因此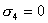 ,且B板外侧场强为零。 ,且B板外侧场强为零。应注意B板内侧 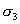 受到A极电荷产生的场影响, 受到A极电荷产生的场影响,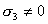 ,对B板内的任一点b的场强应为零,由场强迭加原理 ,对B板内的任一点b的场强应为零,由场强迭加原理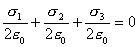 所以 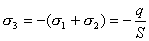 此时又必须满足A板内任意点a场强为零,由场强迭加原理和电荷守恒定律 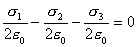 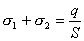 可得 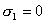 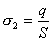 可见B板接地后,AB两板的电荷都分布在金属板内侧,此时两板间电势差 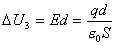 |
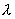 的直线电荷,直线电荷的一端距导体平面距离密度为 的直线电荷,直线电荷的一端距导体平面距离密度为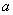 ,如题图12-2所示 ,如题图12-2所示求:(1)垂足o点处的感应电荷面密度; (2)平面上距o点  处P的感应电荷密度; 处P的感应电荷密度;(3)在感应面密度为 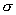 处的导体表面 处的导体表面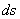 的面积上感应电荷所受的电场力; 的面积上感应电荷所受的电场力; |
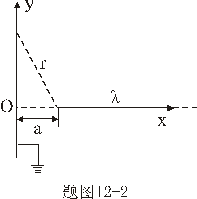 【解】(1) 半无限长直线电荷在垂足o处产生的场强 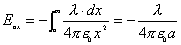 设垂足处导体板感应电荷密度为 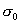 ,导体板内的合场强为零,即 ,导体板内的合场强为零,即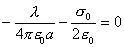 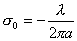 (2)半无限长带电直线在P点处产生的场强的 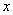 分量为 分量为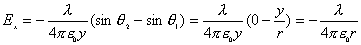 与(1)中情况相似,可得板内的场强为零,即 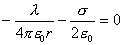 得  (请读者考虑用镜象法求解) (3)我们先求垂足处感应电荷所受的力 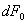 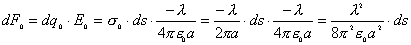 方向沿 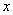 正方向 正方向在位置P处感应电荷所受的电场力 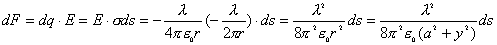 沿 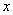 正方向。 正方向。事实上,直接可代金属表面单位面积所受力的公式 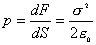 同样可得上述结果。 同样可得上述结果。 |
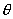 。证明,当 。证明,当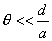 时略去边缘效应,它的电容 时略去边缘效应,它的电容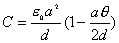 。 。 |
 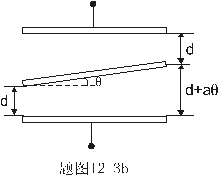 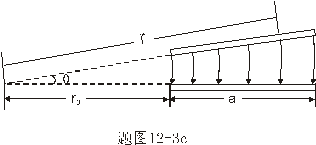 【解】本题通常采用三种解法:(1)电容的并联;(2)电容的串联;(3)从电容的定义出发求解。前两种方法不尽合理,下面就这三种解法作些讨论。 方法一,用电容器并联公式求解 把图1的电容器看作大量细狭条的电容器元并联而成,其中任一电容器元的电容 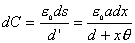 总电容 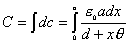 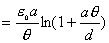 由于题设 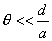 ,即 ,即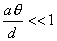 ,上式按泰勒级数展开 ,上式按泰勒级数展开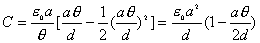 但应注意,这一解法的明显不妥之处有二:其一是每一电容 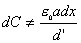 ,而应是两长直导线间的电容;其二是每一对对应狭条之间有自身电容,各狭条电容器元之间还存在着互电容。那么为什么这错误的观点能得出正确的结论呢?由于各狭条电容器元之间的自电容和互电容的相互影响,使两极板间的电力线几乎平行分布,相当于忽略了互电容,而将自电容 ,而应是两长直导线间的电容;其二是每一对对应狭条之间有自身电容,各狭条电容器元之间还存在着互电容。那么为什么这错误的观点能得出正确的结论呢?由于各狭条电容器元之间的自电容和互电容的相互影响,使两极板间的电力线几乎平行分布,相当于忽略了互电容,而将自电容 看作为平行板电容器,这两种错误观点正好互补,以至得出正确的结果,这种“错错得对”的处理方法还是不宜采用的。 看作为平行板电容器,这两种错误观点正好互补,以至得出正确的结果,这种“错错得对”的处理方法还是不宜采用的。方法二,利用电容器的串联公式求解 如图b所示,补上一只与原来那只完全相同的电容器,与原来的那只相串联,串联后的电容  ,原来电容为串联后电容的2倍。 ,原来电容为串联后电容的2倍。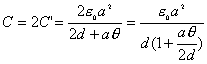 由于 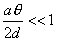 ,上式可近似为 ,上式可近似为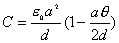 看来这种解法很巧妙,实质上这种解法也是不妥的,因为这两只电容器串联后,中间的那块倾斜的金属板是个等势体,它将影响电力线的分布,电力线并非均匀的平行直线,而每只电容器的电力线应如图3所示的那样分布,因此 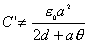 ,那么为什么这种方法也能得出正确的结果呢?因为题设 ,那么为什么这种方法也能得出正确的结果呢?因为题设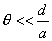 ,电力线的不均匀性不明显,仍近似看作平行直线,相当于把中间倾斜的金属板拿掉了,忽略边缘效应,得出了这种近似下的C后,再经数学的近似处理,正好把答案“凑”对了。因此,这种方法仍不宜采用。 ,电力线的不均匀性不明显,仍近似看作平行直线,相当于把中间倾斜的金属板拿掉了,忽略边缘效应,得出了这种近似下的C后,再经数学的近似处理,正好把答案“凑”对了。因此,这种方法仍不宜采用。方法三,从电容器的定义出发求解 设电容器带电量Q后,两极板的电势差为U,两极板的延长面交线为O轴,由静电场回路定律可知,两极板靠近的那端的电力线比另一端要密,电力线接近于圆弧,如图c所示,在离O轴r处的场强E可表示为 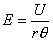 设极板上离O轴距离r处的电荷密度为 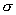 ,则 ,则 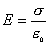 比较以上两式得 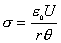 极板上的总电量 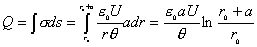 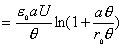 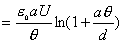 由于 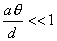 ,将上式按泰勒级数展开 ,将上式按泰勒级数展开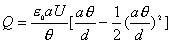 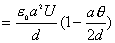 由电容器电容的定义 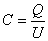 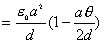 得证。 得证。这第三种方法计算稍繁一些,但比较严谨合理。 |
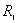 =1厘米的导体球带有电量 =1厘米的导体球带有电量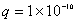 库仑的电量。球外有一内外半径 库仑的电量。球外有一内外半径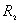 =3厘米, =3厘米,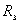 =4厘米的同心导体球壳,壳上带有电量 =4厘米的同心导体球壳,壳上带有电量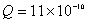 库仑。 库仑。求:(1)内球的电势 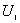 ,外球壳的电势 ,外球壳的电势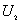 ; ;(2)将内球接地,在外球离地面很远的情况下,外球壳的电势 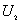 '为多少? '为多少? |
【解】(1)在导体球壳内作包围球壳内表面的高斯面S。球壳内表面感应电荷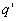 应满足高斯定理: 应满足高斯定理:
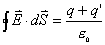 由于导体壳内的 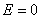 ,所以有 ,所以有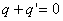 ,即 ,即
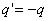 再有电量守恒定律可知,在 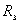 球壳外表面上带电量为 球壳外表面上带电量为 ,这带电系统的电荷分布如题图11-4b所示,由电势迭加原理可求得: ,这带电系统的电荷分布如题图11-4b所示,由电势迭加原理可求得: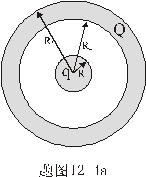  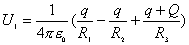 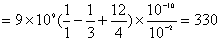 伏 伏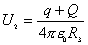 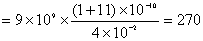 伏 伏(2)内球接地,指的是内球电势为零(不是内球的电量为零)。设接地后内球带电为 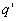 ,类似于图b的电荷分布,只需将 ,类似于图b的电荷分布,只需将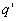 换成 换成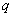 即可,得: 即可,得: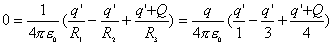 解得: 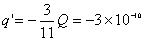 库仑 库仑此情况下导体外壳的电势  伏 伏方法二,可将半径 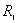 和 和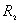 两球面看作为球形电容器,它的电容量 两球面看作为球形电容器,它的电容量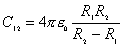 将 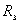 的球面由无穷远处组成相当于孤立导体的电容 的球面由无穷远处组成相当于孤立导体的电容
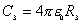 球壳是两电容的共同极板,内球接地,与无穷远处的电势都为零,也相当于共同极板,所以可看作 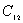 和 和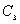 并联。所以,共同带正电的极板Q处,它的电势 并联。所以,共同带正电的极板Q处,它的电势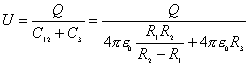 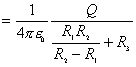 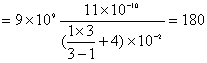 伏 伏
|
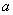 , ,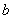 ( (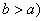 中间充满电导率为 中间充满电导率为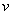 的材料,电导率 的材料,电导率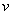 是随外场强变化的,且 是随外场强变化的,且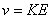 ,其中 ,其中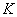 为常数,现将两球壳维持恒定的电压 为常数,现将两球壳维持恒定的电压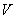 ,求两壳间的电流。 ,求两壳间的电流。 |
【解】由欧姆定律微分形式 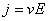 又由题设条件 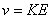 ,所以有 ,所以有  在半径 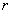 处的总电流 处的总电流 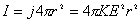 由此得 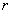 处的电场强度 处的电场强度 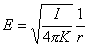 两球壳 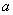 和 和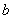 间的电势差 间的电势差 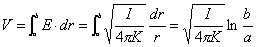 由此解得 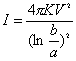 |