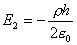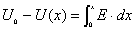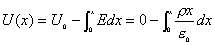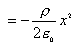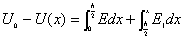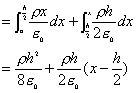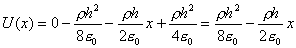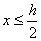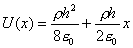【解】我们先在半球面上取一细环,细环上的电荷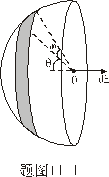 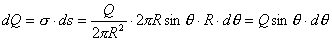 细环在轴线上产生的场强 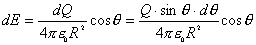 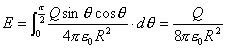 |
||
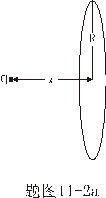  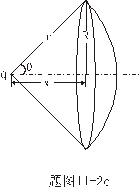 【解】 方法一:如图11-2b所示电力线穿过圆平面上细圆环 ds的通量(在以下计算过程中,应注意到图中x是常量。) 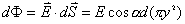 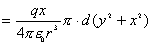 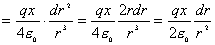 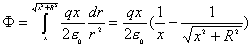 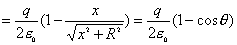 式中 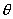 如图c中所示。 如图c中所示。方法二:如图c所示,穿过圆平面的电通量与穿过图示球冠的电通量相等。穿过包围点电荷q闭合球面的总电量为 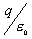 ,再由球冠面积S=2 ,再由球冠面积S=2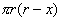 占总球面面积 占总球面面积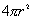 中的比率,就可求出球冠的电通量。由此求得圆平面的电通量: 中的比率,就可求出球冠的电通量。由此求得圆平面的电通量: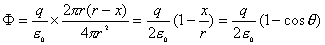
|
||
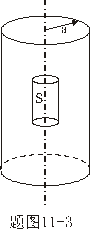
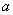 的无限长带电圆柱体,其体电荷密度 的无限长带电圆柱体,其体电荷密度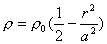 ,其中 ,其中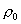 为常数, 为常数,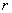 为离圆柱体轴线的距离。试求: 为离圆柱体轴线的距离。试求:(1)圆柱体内外各处的电场强度。 (2)求出场强最大值的位置在何处,场强多大? (3)求轴线处的电势。 |
||
|
||
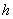 的无限大平板型区域中均匀分布着电荷,电荷体密度为 的无限大平板型区域中均匀分布着电荷,电荷体密度为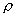 。 。(1)求板内外场强的分布,并画出场强分布曲线 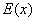 ; ;(2)若取中心面的电势为零,试求任意位置处的电势,并画出相应的电势分布曲线 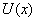 。 。 |
||
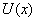 曲线分布图11-4c 曲线分布图11-4c下面再看一看这场强曲线和电势曲线间的相互关系。 在 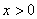 的区域场强 的区域场强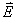 沿 沿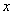 正方向;在 正方向;在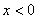 的区域场强 的区域场强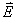 是沿着 是沿着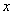 的负方向。场强的方向应是电势降落的方向,在 的负方向。场强的方向应是电势降落的方向,在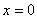 处 处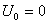 ,因此整个区域内的电势都为负值。还应注意到电势曲线上的斜率的负值应等于场强的大小,也就是场强大的位置电势曲线的斜率大,即电势的变化率大,场强小的地方电势的变化率小。场强为零的位置为电势的极值位置。 ,因此整个区域内的电势都为负值。还应注意到电势曲线上的斜率的负值应等于场强的大小,也就是场强大的位置电势曲线的斜率大,即电势的变化率大,场强小的地方电势的变化率小。场强为零的位置为电势的极值位置。 |
||
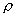 的球体内,有一球形空腔,如题图11-5a所示,我们将坐标原点建立在球心上,空腔球心的位置矢量为 的球体内,有一球形空腔,如题图11-5a所示,我们将坐标原点建立在球心上,空腔球心的位置矢量为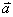 。 。(1)试求空腔内任意点的场强。 (2)若球体半径为 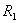 ,空腔半径为 ,空腔半径为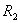 ,试求空腔球心处的电势 ,试求空腔球心处的电势 |
||
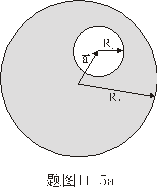 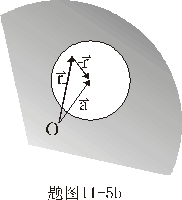
【解】(1) 我们采用补偿方法来求解,设想原球体没有空腔,为正体电荷 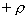 充满,而再设想在空腔位置放体电荷 充满,而再设想在空腔位置放体电荷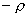 的 的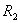 球体,正、负体电荷相消,相当于一空腔。 球体,正、负体电荷相消,相当于一空腔。利用高斯定理可求均匀带电(没有空腔的)球体内的任意点的场强。 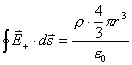 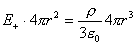 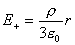 写成矢量式: 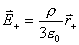 同理可证负电荷均匀带电球体,在位置矢量 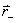 处产生的场强 处产生的场强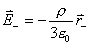 在空腔内任意点 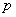 处的场强,为均匀带电正负球体场强的矢量和(见图b) 处的场强,为均匀带电正负球体场强的矢量和(见图b)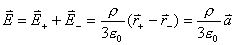 可见空腔内为一均强电场,电场的方向与 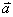 方向相同。 方向相同。(2)我们先求没有空腔时球体半径为 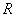 的球体 的球体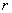 处的电势。 处的电势。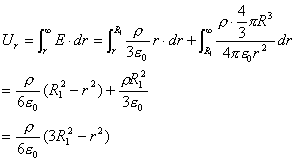 没有空腔情况下正电荷均匀带电球体在位置矢量 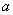 处的电势 处的电势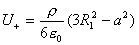 均匀带体电荷 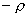 的球体对球心产生的电势为 的球体对球心产生的电势为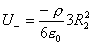 由此我们由电势迭加原理求得空腔球心处的总电势 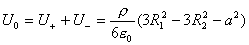 |
||
【例11-6】已知电场中的电势随x的变化曲线如题图11-6a所示,其中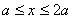 区间内的曲线是抛物线,AB和CE分别是抛物线上A点和C点处的切线。 区间内的曲线是抛物线,AB和CE分别是抛物线上A点和C点处的切线。(1)画出 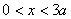 区间内的电场分布曲线; 区间内的电场分布曲线;(2)试求 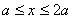 区间内的电荷分布。 区间内的电荷分布。 |
||
| 【解】(1)根据场强为电势的负梯度关系: 在 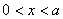 , ,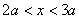 的区域, 的区域,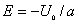 。 。在 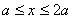 区域电势曲线为抛物线,作为它的负梯度,场强曲线为直线,直线两端的场强分别为 区域电势曲线为抛物线,作为它的负梯度,场强曲线为直线,直线两端的场强分别为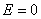 , ,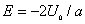 ,相应的场强函数为: ,相应的场强函数为: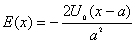 由此可画出场强E随x变化的曲线图b。  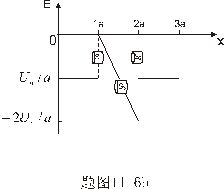 (2)根据高斯定理,静电荷是电力线的源头或尾间。由电场分布可见。 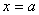 、 、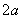 处出现场强突变,该处应有面电荷, 处出现场强突变,该处应有面电荷,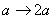 之间场强线性变化,该区域有体电荷。 之间场强线性变化,该区域有体电荷。作圆柱形高斯面 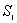 ,其左底面在 ,其左底面在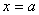 处的左侧,其右底面在 处的左侧,其右底面在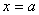 处的右侧,见图b,其左、右底面上场强分别为 处的右侧,见图b,其左、右底面上场强分别为 、0。由高斯定理: 、0。由高斯定理: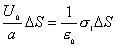 得面电荷密度: 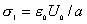 同法求解 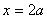 处面电荷密度,对高斯面 处面电荷密度,对高斯面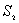 有 有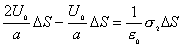 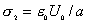 作圆柱形高斯面 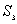 ,见图b,两底面均在 ,见图b,两底面均在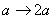 区间内,对 区间内,对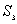 应用高斯定理: 应用高斯定理: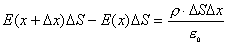 移项整理并取极限,得  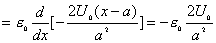 可见在 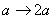 区间内电荷体密度 区间内电荷体密度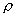 是与位置无关的均匀负电荷。 是与位置无关的均匀负电荷。
|
||
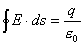 (1)
(1)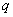 可通过体电荷积分求得:
可通过体电荷积分求得: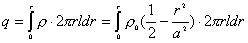
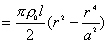
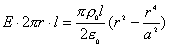
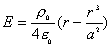 (2)
(2)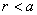 时,
时,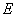 为正,即沿半径方向向外
为正,即沿半径方向向外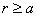 时,即圆柱体外场强为0
时,即圆柱体外场强为0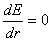
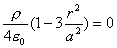
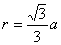 处场强最大,代入(2)式得场强的最大值
处场强最大,代入(2)式得场强的最大值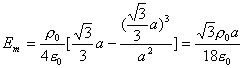
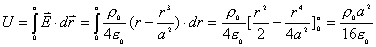
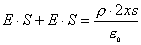
 得:
得:
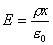
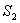 ,由高斯定理
,由高斯定理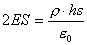
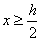 , 得
, 得 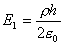
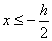 , 得
, 得