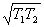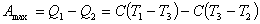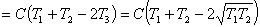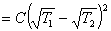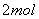 氦气,下室盛 氦气,下室盛 氢气,上部活塞上放有砝码,可保持上室内气体压强不变。若开始时两室气体温度均为 氢气,上部活塞上放有砝码,可保持上室内气体压强不变。若开始时两室气体温度均为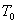 ,下室容积为 ,下室容积为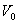 ,现缓慢地将下室活塞向上推。 ,现缓慢地将下室活塞向上推。求:(1)试求下方气体的摩尔热容和多方指数; (2)当下室容积减半时,试求下方气体做的功和上方气体的内能变化。 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
 的循环,并已求得如表中所填的三个数据,你能根据热力学定律和循环过程的特点,把表填完整吗? 的循环,并已求得如表中所填的三个数据,你能根据热力学定律和循环过程的特点,把表填完整吗? |
||||||||||||||||||||||||||||||||||||||||||||||||
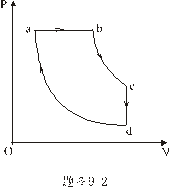 【解】a—b等压过程 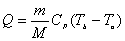 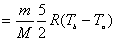 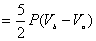 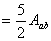 得: 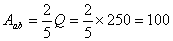 焦耳 焦耳由热力学第一定律 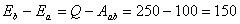 焦耳 焦耳b—c绝热过程中 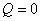 , ,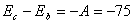 焦耳 焦耳d—a等温过程中 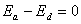 , ,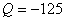 焦耳 焦耳对整个循环过程 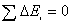 ,可得 ,可得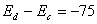 焦耳 焦耳c—d等容过程中 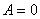 , ,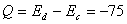 焦耳 焦耳整个循环的功 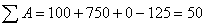 焦耳 焦耳由此得循环效率  最后请看填好后的表
|
||||||||||||||||||||||||||||||||||||||||||||||||
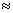 100焦耳) 100焦耳) |
||||||||||||||||||||||||||||||||||||||||||||||||
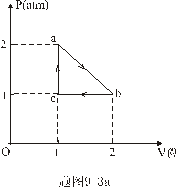 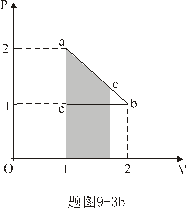 【解】这三角形abc循环过程作的净功为这三角形所包围的面积。 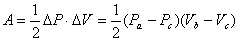 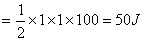 (1) (1)在循环过程中bc为放热过程,本题中不必计算;ca为等容吸热过程。它吸热 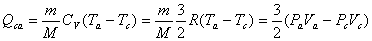 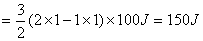 对于ab这过程并不是净吸热,首先要判别这过程中从吸热转化为放热的位置e。参阅图9-3b。由热力学第一定律的微分形式: 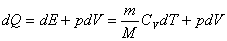 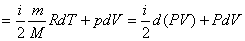 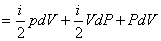 a到b过程中由吸热转化为放热位置e的条件为 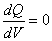 ,由上式得: ,由上式得: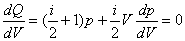 即: 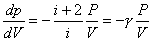 (2) (2)这说明ab过程中的e点处恰与一绝热线相切。ab直线过程方程满足: 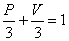 或 或
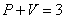 (3) (3)由直线方程可得 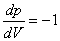 (4) (4)又单原子理想气体的 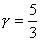 代入(2),解(2)(3)(4)式得e的位置 代入(2),解(2)(3)(4)式得e的位置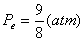 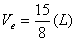 系统从a到e的过程中吸收热量 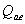 可由热力学第一定律来求: 可由热力学第一定律来求: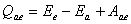 式中  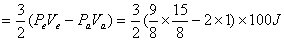 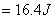 在ae过程中所作的功,可用ae过程方程下方的梯形面积来计算: 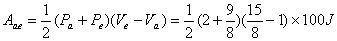 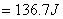 得ae过程中吸热 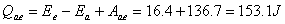 循环过程所吸热 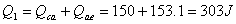 由此得循环效率 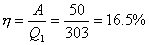 |
||||||||||||||||||||||||||||||||||||||||||||||||
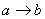 , ,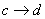 , ,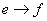 为等温过程,其温度分别为: 为等温过程,其温度分别为: , ,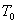 , ,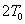 ; ;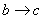 , ,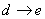 , ,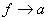 为绝热过程。设 为绝热过程。设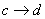 过程曲线下的面积为 过程曲线下的面积为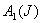 , ,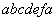 循环过程曲线所包围的面积为 循环过程曲线所包围的面积为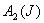 。求:该循环的效率。 。求:该循环的效率。 |
||||||||||||||||||||||||||||||||||||||||||||||||
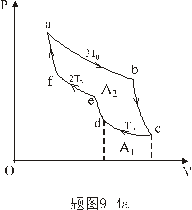 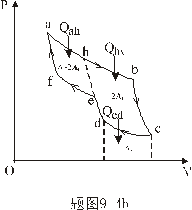 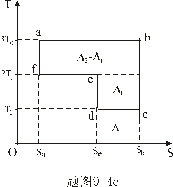 【解】方法一,分成两卡诺循环,如图b所示,再利用卡诺循环特点解。 在卡诺循环 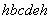 中 中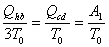 得: 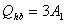 得  面积为 面积为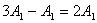 可得卡诺循环  所作的功,这功为其循环曲线所包围的面积 所作的功,这功为其循环曲线所包围的面积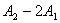 。再根据卡诺机效率 。再根据卡诺机效率即 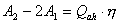 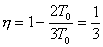 可知 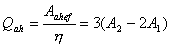 整个 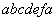 循环中所吸热 循环中所吸热 得循环效率 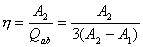 方法二,根据循环过程的特点,熵是态函数的特点求解。 循环一周系统的熵变 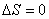 , ,即: 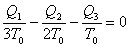 (1) (1)系统净吸热为系统对外所作的净功: 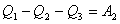 (2) (2)仍有 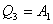 (3) (3)同样解得 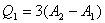 与方法一结果相同。 与方法一结果相同。方法三,用温熵图求解 正确画出该循环的温熵图c,可简洁醒目地直接地看出等温ab过程中吸收的热量 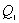 , ,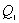 的大小为ab等温线下方的面积。这就方便地由图c得到 的大小为ab等温线下方的面积。这就方便地由图c得到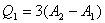 。 。
|
||||||||||||||||||||||||||||||||||||||||||||||||
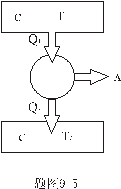
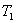 和 和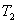 ,热容量与温度无关均为C,有一热机工作这两热源之间,直至两热源具有共同的温度为止。求这热机能输出的最大功为多少? ,热容量与温度无关均为C,有一热机工作这两热源之间,直至两热源具有共同的温度为止。求这热机能输出的最大功为多少? |
||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
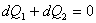
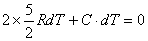
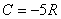
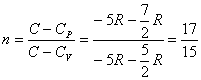
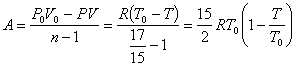
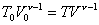 ,
,
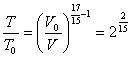 代入上式, 得:
代入上式, 得: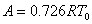
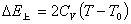
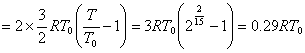

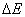
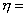
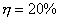
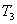 ,则系统的总熵变为:
,则系统的总熵变为: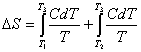
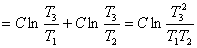 (1)
(1)