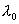 ,木板静止在平衡位置处;在木板上方高 ,木板静止在平衡位置处;在木板上方高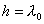 处自由落下一与木板质量相同的泥块,它与木板作完全非弹性碰撞, 处自由落下一与木板质量相同的泥块,它与木板作完全非弹性碰撞,(1)写出碰撞后木板的运动方程。 (2)求从泥块与木板相碰到它们第一次回到相碰位置所用的时间。 (3)求任一位置处泥块与木块间的相互作用力。 |
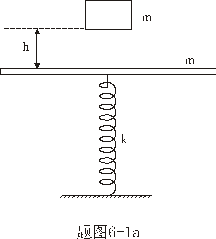 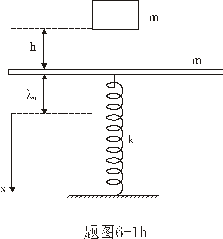 【解】(1)题为竖直放置的弹簧振子,其解为: 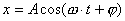 本题就是根据具体的条件确定谐振动方程中的 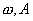 和 和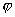 。 。 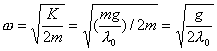 再由初始条件确定 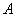 和 和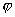 。 。碰撞后泥块与木板的平衡位置已不是原来木板的平衡位置了,而应满足: 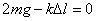 得: 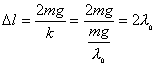 即在原来木板平衡位置下方 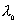 位置处,我们如图b取坐标,新的平衡位置为坐标原点,x轴向下,则泥块与木板碰撞瞬时的位置 位置处,我们如图b取坐标,新的平衡位置为坐标原点,x轴向下,则泥块与木板碰撞瞬时的位置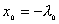 。 。泥块与木板碰撞瞬时满足动量守恒定律: 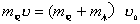 即 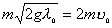 ,得 ,得 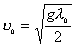 由此得: 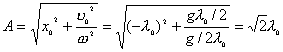 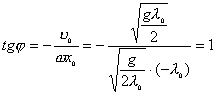 得: 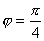 或 或 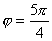 因为 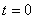 时 时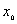 为负, 为负,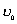 为正 为正应取: 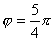 或取 或取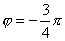 这里如果用参考圆的方法,由图c就一目了然了。碰撞后木板的谐振动方程为: 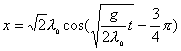  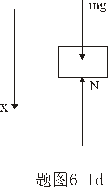 (2)木板经过最低点第一次回到原来位置 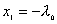 应有 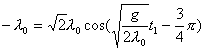 即 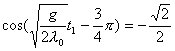 那么 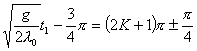 
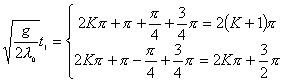 分析上式 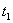 为大于零的最小值应: 为大于零的最小值应: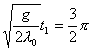 即: 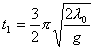 用上解析分析是比较麻烦的,如采用参考圆就方便许多了,再参见图6-1c,可见 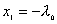 , ,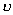 为负,为第二象限角,又参考圆半径为 为负,为第二象限角,又参考圆半径为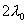 ,所以 ,所以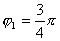 。 。参考圆旋转矢量以匀角速度 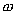 转动,可求得: 转动,可求得: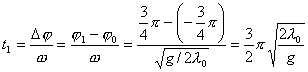 事实上从参考圆中可以看出旋转矢量矢端转过 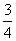 个圆周,所以用时为: 个圆周,所以用时为: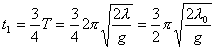 (3)泥块的分离体受力图如图所示,列出相应的牛顿力学方程: 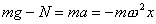 相互作用力 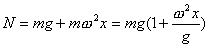 可见x取正,即在平衡位置下方,相互作用力比泥块的重量大;而x取负,即在平衡位置上方相互作用力比泥块小。 在最下方 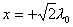 时 时最大相互作用力: 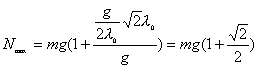 在最上方 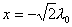 时 时最小相互作用力 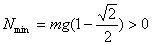 由此可知在整个谐振动过程中泥块不会跳离木板。 本题如坐标向上取,请读者考虑一下计算的结果有何不同? |
 和 和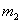 的二物块。它们之间被一根倔强系数为 的二物块。它们之间被一根倔强系数为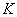 的轻弹簧连接着,试求该系统的振动周期。 的轻弹簧连接着,试求该系统的振动周期。 |
【解】方法一,取如图a所示的坐标,设弹簧原长为 ,系统在振动过程中某时刻物块 ,系统在振动过程中某时刻物块 和 和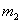 的坐标分别为 的坐标分别为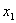 和 和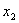 ,如图所示,分别对 ,如图所示,分别对 和 和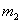 列出运动微分方程。 列出运动微分方程。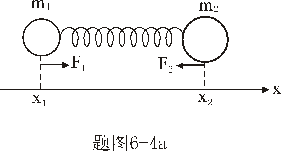 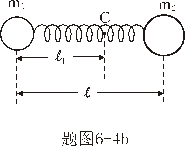 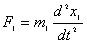 (1)
(1)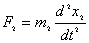 (2)
(2)又  (1)式(2)式分别改写成: 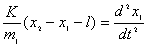 (3) (3)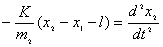 (4) (4)(4)式减(3)式: 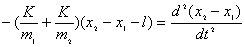 令 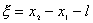 上式可改写为: 上式可改写为: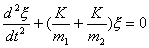 由此得该系统的谐振动周期: 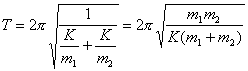 方法二,在质心坐标系解:我们先讨论一下弹簧的长度与倔强系数的关系,设弹簧原长为  ,剪短以后的弹簧长为 ,剪短以后的弹簧长为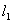 ,在相同力 ,在相同力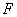 作用下,剪短后的弹簧 作用下,剪短后的弹簧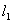 的伸长量为 的伸长量为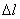 ,就要比原弹簧来得小。由弹簧的倔强系数定义: ,就要比原弹簧来得小。由弹簧的倔强系数定义:原来弹簧的倔强系数: 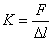 剪短后弹簧的倔强系数: 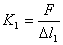 上二式相比余: 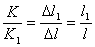 可知同一种弹簧它的倔强系数与它原长成反比。 由题意可知,弹簧对  和 和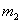 的作用力是系统的内力,系统在谐振动过程中质心 的作用力是系统的内力,系统在谐振动过程中质心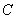 的位置相当于被固定不动,作用于 的位置相当于被固定不动,作用于 的弹簧长度 的弹簧长度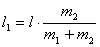 又根据上面讨论 又根据上面讨论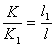 所以作用于  物块的弹簧倔强系数 物块的弹簧倔强系数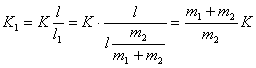 所以对于质量为  物块的弹簧振子的振动周期 物块的弹簧振子的振动周期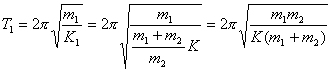 同理 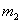 的弹簧振子周期 的弹簧振子周期 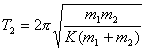 方法三,能量法解: 仍取如a图的坐标系,系统总机械能为: 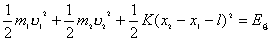 上式对时间 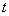 求导得: 求导得: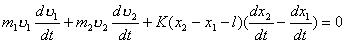 即 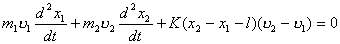 (5) (5)由于系统合外力等于零,系统动量守恒,因此 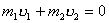 ,即 ,即
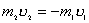 将(5)式除以  ,得: ,得: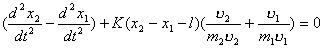 即 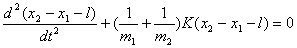 令 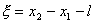 ,上式与方法一中的微分方程一样,同样得: ,上式与方法一中的微分方程一样,同样得: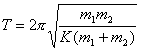 |
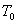 ,现将该弹簧振子浸入水中,由于水的阻尼作用,经过每个周期振幅降为原来的90%,求 ,现将该弹簧振子浸入水中,由于水的阻尼作用,经过每个周期振幅降为原来的90%,求(1)求振子在水中的振动周期 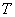 (2)如果开始时振幅 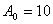 厘米,阻尼振动从开始到振子静止求振子经过的路程为多少? 厘米,阻尼振动从开始到振子静止求振子经过的路程为多少? |
【解】(1)由题意知 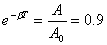 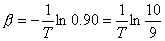 又阻尼振动的圆频率: 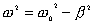 即 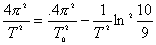 即 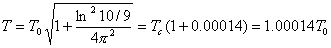 从本题解中可知阻尼因子对振幅的影响是比较大的,而对振动的周期影响却很小,有时甚至可以忽略不计。 (2)在整个阻尼振动过程中,振子所经过的路程可近似地表示为: 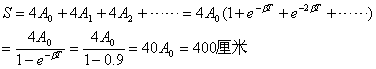 |
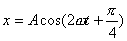 和 和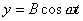 的李萨如图形: 的李萨如图形: |
【解】一般采用参考圆的方法来确定任一时刻振动质点的坐标,具体做法如题图所示。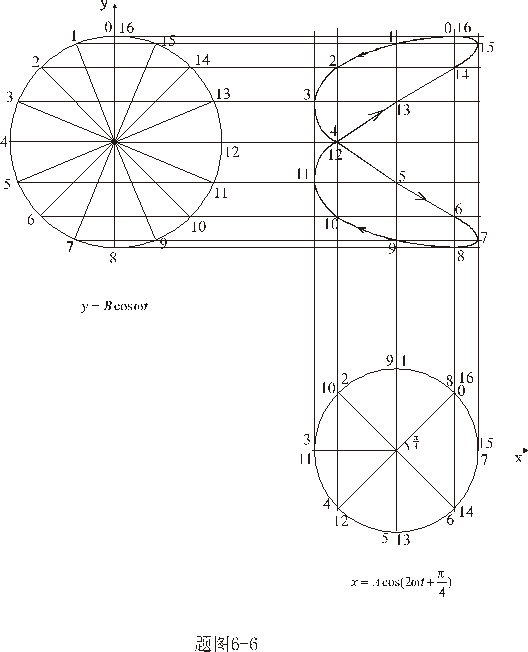
|
| |