物体受到的合外力或合外力矩为零的位置,我们称之为平衡位置。当物体偏离平衡位置时,物体受到与位移成正比与位移方向相反的恢复力(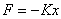 ),或受到与角位移成正比与角位移方向相反的恢复力矩( ),或受到与角位移成正比与角位移方向相反的恢复力矩(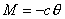 )作用时物体将作谐振动。 )作用时物体将作谐振动。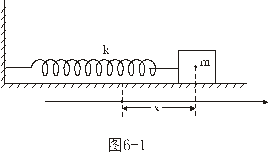 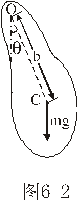 1、弹簧振子(图6-1) 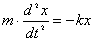 这微分方程的解为: 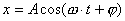 式中圆频率  由此可得振动周期 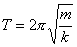 2、复摆(物理摆) 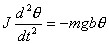 式中b为支点到质心的距离,也常用 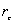 表示。 表示。这微分方程的解为: 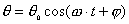 式中圆频率 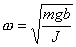 ,由此可得振动周期 ,由此可得振动周期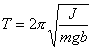 3、其他类型简谐振动的一般求解步骤: (1)选取合适的坐标,找出平衡位置。 (2)写出在平衡位置处物体所受各力的平衡条件,(在此较简单的情况下这一步可省略)。 (3)给一微扰使物体偏离平衡位置,画出物体的受力图,找出回复力或回复力矩的表达式。 (4)列出动力学微分方程,与标准谐振动微分方程比较系数,可得谐振动的圆频率和周期。 |
1、解析式 谐振动的运动方程为 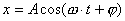 将此式分别对时间求一次,二次导数可相应得到振子的速度 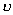 和加速度a随时间的函数表达式: 和加速度a随时间的函数表达式:
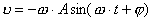 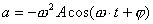 事实上速度 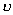 和加速度a还应是位移x的函数: 和加速度a还应是位移x的函数: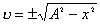 , , 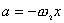 在运动方程中圆频率 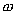 或周期T是由力学条件所确定的,而振幅A和初相位 或周期T是由力学条件所确定的,而振幅A和初相位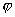 是由初始条件所确定的。将 是由初始条件所确定的。将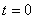 代入位移 代入位移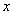 和速度 和速度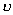 的表达式可得: 的表达式可得: 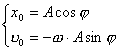 由此可解出: 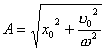 , , 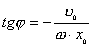 2、用旋转矢量(即参考圆)描述 旋转矢量 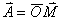 ,以匀角速 ,以匀角速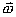 逆时针旋转,矢端M点在X轴上的投影P点的运动方程: 逆时针旋转,矢端M点在X轴上的投影P点的运动方程: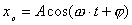 却好是谐振动方程,且M点匀速圆周运动的速度 却好是谐振动方程,且M点匀速圆周运动的速度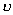 和加速度 和加速度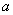 在X轴上的投影 在X轴上的投影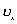 和 和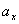 也却好是P点在X轴上作谐振动的速度和加速度。所以用参考圆来描述谐振动比较简单直观,容易记忆(如图6-3所示)。 也却好是P点在X轴上作谐振动的速度和加速度。所以用参考圆来描述谐振动比较简单直观,容易记忆(如图6-3所示)。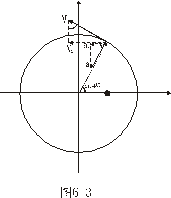 3、用谐动图线描述 谐振动的位移、速度和加速度随时间变化的曲线如图 4 所示。一般要求看懂位移x和速度 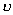 和加速度 和加速度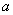 三条曲线的相位关系依次超前 三条曲线的相位关系依次超前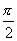 。 。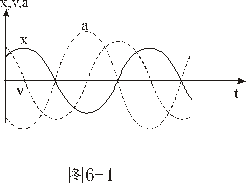 |
 三、谐振动的能量 三、谐振动的能量 |
弹性势能: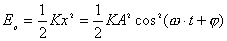 动能: 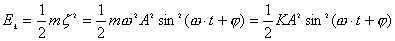 弹簧振子系统的总能量: 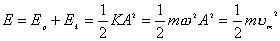 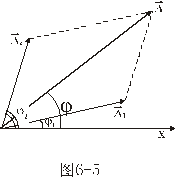 |
 四、谐振动的合成 四、谐振动的合成 |
1、同方向同频率两个谐振动的合成 设谐振动 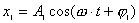 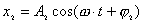 合成后的谐振动 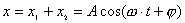 式中: 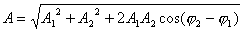 ; ; 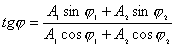 此关系式用旋转矢量图6-5则很容易理解和记忆。 当:  则
则 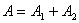 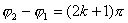 则 则
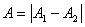 2、同方向频率相近的谐振动合成 合成后的圆频率为其平均圆频率 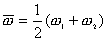 或其频率 或其频率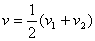 ,合成后产生的拍频 ,合成后产生的拍频
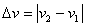 。 。3、互相垂直的谐振动合成 两个相互垂直的同频率谐振动合成的质点运动轨迹一般为椭圆,在一定条件下也可能为圆或直线。轨迹的形状决定于两振动的相位差与振幅,当两个谐振动频率不相等,但有简单的整数比时,质点的运动轨迹为李萨如图形。 |
 五、阻尼振动 五、阻尼振动 |
当弹簧振子在振动过程中受到的阻力与速度大小成正比与速度方向相反的阻力作用时,振子的动力学方程为: 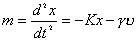 式中 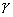 为阻尼系数。若令 为阻尼系数。若令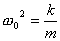 , ,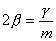 则上式可改写为: 则上式可改写为: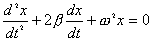 在小阻尼情况下,即 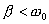 的条件下其微分方程的解为: 的条件下其微分方程的解为: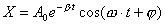 ,其中 ,其中
 ;可得周期 ;可得周期 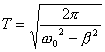 在大阻尼情况下(即 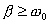 )就不再是周期运动了。 )就不再是周期运动了。 |
 六、有阻尼的受迫振动 六、有阻尼的受迫振动 |
有阻尼的受迫振动的动力学方程为: 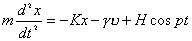 式中H为强迫力的最大值,p为强迫力的圆频率。若令 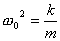 ; ;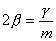 ; ;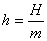 上式可写为: 上式可写为: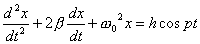 该微分方程的解为: 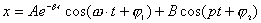 前项就是阻尼振动,随时间 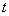 的增加而很快消失,后项是稳定的振动,其中振幅B由下式表示: 的增加而很快消失,后项是稳定的振动,其中振幅B由下式表示: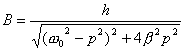 由此式可知当强迫力频率 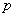 与固有频率 与固有频率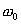 相差很大时强迫振动振幅就很小,而强迫力频率 相差很大时强迫振动振幅就很小,而强迫力频率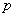 和固有频率接近时,强迫振动的振幅就很大,这种情况称之谓共振。 和固有频率接近时,强迫振动的振幅就很大,这种情况称之谓共振。 |