 4.2 如图所示的圆锥摆,绳长为 4.2 如图所示的圆锥摆,绳长为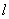 ,绳子一端固定,另一端系一质量为m的质点,以匀角速 ,绳子一端固定,另一端系一质量为m的质点,以匀角速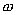 绕铅直轴线作圆周运动,绳子与铅直线间的夹角为 绕铅直轴线作圆周运动,绳子与铅直线间的夹角为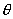 。在质点旋转一周的过程中,试求: 。在质点旋转一周的过程中,试求:(1)质点所受合外力的冲量 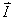 ; ;(2)质点所受张力T的冲量 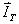 。 。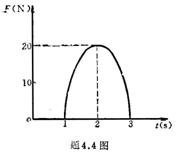 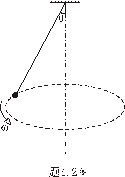  4.4 —物体在多个外力作用下作匀速直线运动,速度 4.4 —物体在多个外力作用下作匀速直线运动,速度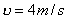 。已知其中一力 。已知其中一力 方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图所示。求: 方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图所示。求:(1)力  在 在 到 到 间所做的功; 间所做的功;(2)其他力在 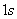 到 到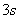 间所做的功。 间所做的功。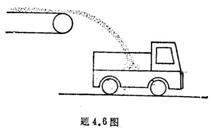  4.6 一运煤的传送带以 4.6 一运煤的传送带以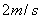 的恒定水平速率传动,每秒运煤20kg。若传送带与运输车厢高度差为0.8m,且运输车静止不动,求煤对运输车的冲力。(取 的恒定水平速率传动,每秒运煤20kg。若传送带与运输车厢高度差为0.8m,且运输车静止不动,求煤对运输车的冲力。(取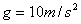 )。 )。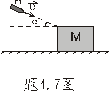  4.7 水平桌面上放一质量为M的木块,木块与桌面间的摩擦系数为 4.7 水平桌面上放一质量为M的木块,木块与桌面间的摩擦系数为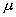 ,现有一质量为m的子弹与水平面成 ,现有一质量为m的子弹与水平面成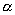 ,方向以速度 ,方向以速度 击中木块,并留在木块里。求:子弹和木块速度能到达多大的共同水平速度V? 击中木块,并留在木块里。求:子弹和木块速度能到达多大的共同水平速度V? 4.10 一物体在光滑的水平面上以速度 4.10 一物体在光滑的水平面上以速度 沿x正方向运动,突然由于内部作用在水平面内分裂成A、B、C三个碎片,它们的质量为 沿x正方向运动,突然由于内部作用在水平面内分裂成A、B、C三个碎片,它们的质量为 。取物体分裂处为坐标原点,经 。取物体分裂处为坐标原点,经 后其中两个碎片的位置为A(15,-6)和C(4,9),试求B碎片的位置。 后其中两个碎片的位置为A(15,-6)和C(4,9),试求B碎片的位置。 4.11 质量为M,长为L的细绳在水平面内以角速度 4.11 质量为M,长为L的细绳在水平面内以角速度 绕O点匀速转动,如图所示。试用下述两种方法计算离中心r处的绳子张力: 绕O点匀速转动,如图所示。试用下述两种方法计算离中心r处的绳子张力:(1)牛顿运动定律; (2)质心运动定理。    4.14 大小相同,质量分别为 4.14 大小相同,质量分别为 和 和 的A、B两球,系在一细柔绳的两端,放在光滑的水平桌面上,细绳被两球拉直在两球的联心线上,如图所示。当B球受到一大小未知,方向与x轴成 的A、B两球,系在一细柔绳的两端,放在光滑的水平桌面上,细绳被两球拉直在两球的联心线上,如图所示。当B球受到一大小未知,方向与x轴成 角度,通过B球中心的水平冲量作用时,获得大小为 角度,通过B球中心的水平冲量作用时,获得大小为 的速度。忽略细柔绳的质量和变形,试求B球的速度方向和作用在B球上冲量 的速度。忽略细柔绳的质量和变形,试求B球的速度方向和作用在B球上冲量 的大小。 的大小。 4.15 质量为m的球,从质量为M的面圆弧形槽中静止下滑,设圆弧形槽的半径为R,如图所示。若所有摩擦都可忽略,求小球刚离开圆弧形槽时,小球和木块速度各是多少? 4.15 质量为m的球,从质量为M的面圆弧形槽中静止下滑,设圆弧形槽的半径为R,如图所示。若所有摩擦都可忽略,求小球刚离开圆弧形槽时,小球和木块速度各是多少?   4.16 质量 4.16 质量 的框子,用一弹簧悬挂起来,弹簧伸长0.10m。现有质量 的框子,用一弹簧悬挂起来,弹簧伸长0.10m。现有质量 的油灰由距离框底0.30m的高处自由落到框上,如图所示。求油灰冲撞框子而使框向下移动的最大距离。 的油灰由距离框底0.30m的高处自由落到框上,如图所示。求油灰冲撞框子而使框向下移动的最大距离。 4.18 质量为 4.18 质量为 和 和 的两个自由质点相互吸引,引力与其质量的乘积成正比,与距离的平方成反比,比例常数为k。开始时,两质点都处于静止状态,其间距为 的两个自由质点相互吸引,引力与其质量的乘积成正比,与距离的平方成反比,比例常数为k。开始时,两质点都处于静止状态,其间距为 ,试求两质点距离为 ,试求两质点距离为 时两质点的速度。 时两质点的速度。 4.19 光滑水平路面上有一质量为 4.19 光滑水平路面上有一质量为 的无动力小车以匀速率 的无动力小车以匀速率 向前行驶,小车由轻绳与另一质量 向前行驶,小车由轻绳与另一质量 的车厢连接,车厢前端放有一质量 的车厢连接,车厢前端放有一质量 的物体,物体与车厢间的摩擦系数为 的物体,物体与车厢间的摩擦系数为 ,如图所示。开始时,车厢静止,绳未拉紧,试求: ,如图所示。开始时,车厢静止,绳未拉紧,试求:(1)当小车、车厢、物体以共同速度运动时,物体相对车厢的位移; (2)从绳子拉紧到小车、车厢与物体具有共同速度所需要的时间(取  )。 )。  4.23 如图所示,光滑水平面上有两只相同的光滑钢球,开始时A球沿x轴以动量 4.23 如图所示,光滑水平面上有两只相同的光滑钢球,开始时A球沿x轴以动量 运动, B球静止在 运动, B球静止在 , , 的位置。当A、B发生碰撞之后,B球动量的大小 的位置。当A、B发生碰撞之后,B球动量的大小 ,试在图b中画出A球所受到的冲量和碰撞后A球的动量。 ,试在图b中画出A球所受到的冲量和碰撞后A球的动量。   4.24 某人以恒力 4.24 某人以恒力 拉煤车时,由于煤车底部出现漏洞,煤粉以 拉煤车时,由于煤车底部出现漏洞,煤粉以 的速率漏掉。设煤车原来静止,质量为 的速率漏掉。设煤车原来静止,质量为 ,自 ,自 时刻开始拉车,同时出现漏煤现象,忽略煤车与地面之间的摩擦,试求 时刻开始拉车,同时出现漏煤现象,忽略煤车与地面之间的摩擦,试求 时刻煤车的速率。 时刻煤车的速率。 4.25 质量为6000kg的火箭,竖直发射,假定喷气速度为1000m/s,问每秒内必须喷出多少气体,才能满足下列条件: 4.25 质量为6000kg的火箭,竖直发射,假定喷气速度为1000m/s,问每秒内必须喷出多少气体,才能满足下列条件:(1)能克服火箭重量所需要的推力; (2)能使火箭最初向上的加速度为  。 。 4.26 火箭以第二宇宙速度 4.26 火箭以第二宇宙速度 沿地球表面切向飞出,在飞离地球过程中,火箭发动机停止工作,不计空气阻力,求火箭在距地心4R的A处的速度。 沿地球表面切向飞出,在飞离地球过程中,火箭发动机停止工作,不计空气阻力,求火箭在距地心4R的A处的速度。   4.28 在光滑的水平桌面上,放有一质量为M的木块,木块与一轻弹簧相连,弹簧的另一端固定在O点上,其劲度系数k。一质量为m的子弹以初速度 4.28 在光滑的水平桌面上,放有一质量为M的木块,木块与一轻弹簧相连,弹簧的另一端固定在O点上,其劲度系数k。一质量为m的子弹以初速度 射向M,并嵌在木块内,初始时弹簧原长为 射向M,并嵌在木块内,初始时弹簧原长为 ,撞击之后木块M运动,到B点时,弹簧长度为L。求在B点时木块的运动速度 ,撞击之后木块M运动,到B点时,弹簧长度为L。求在B点时木块的运动速度 的量值及与弹簧OB的夹角。 的量值及与弹簧OB的夹角。 |