1.氢原子光谱的规律性 |
原子发光是重要的原子现象之一。由于光学仪器的精确性,光谱学的数据对物质结构的研究具有重要的意义。人们对原子光谱曾进行长时期的深入研究,积累了大量观测资料,并根据这些资料的分析,得出有关原子光谱的重要规律。
图13-15是氢原子的光谱图,图中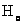 、 、 、 、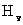 、…等谱线的波长经光谱学的测定已表明在图中。 、…等谱线的波长经光谱学的测定已表明在图中。
1885年,瑞士一中学教师巴耳末(J.J.Balmer)首先将氢原子光谱线的波长用一个简单的公式来表示:
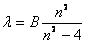 (13-19) (13-19)
式中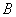 是常量,其量值等于 是常量,其量值等于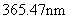 , ,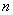 为正整数。当n=3,4,5,…时,上式分别给出氢光谱中 为正整数。当n=3,4,5,…时,上式分别给出氢光谱中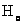 、 、 、 、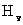 、…等谱线的波长。在光谱学中,谱线也常用频率 、…等谱线的波长。在光谱学中,谱线也常用频率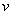 ,或用波数(波长的倒数) ,或用波数(波长的倒数)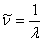 来表征。 来表征。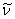 的意义是单位长度内所含有的波的数目。这样,上式可以改写为 的意义是单位长度内所含有的波的数目。这样,上式可以改写为
 (13-20) (13-20)
后人称这个公式为巴耳末公式,而将它所表达的一组谱线称为氢原子光谱的巴耳末系。 |

图13-15 氢原子光谱巴耳末系的谱线
|
1889年,里德伯(J.R.Rydberg)提出了一个普遍的方程,即把式(13-20)中的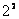 换成其他整数的平方,就可以得出氢原子光谱的其他线系,这方程是 换成其他整数的平方,就可以得出氢原子光谱的其他线系,这方程是
称为里德伯方程,其中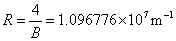 ,称为里德伯常量。氢原子光谱各谱系的名称分别为 ,称为里德伯常量。氢原子光谱各谱系的名称分别为
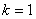 , , 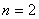 , ,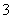 ,…莱曼(T.Lyman)系,(1914年),紫外区 ,…莱曼(T.Lyman)系,(1914年),紫外区
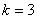 , ,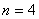 , ,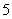 ,…帕邢(F.Paschen)系,(1908年),红外区 ,…帕邢(F.Paschen)系,(1908年),红外区
 , ,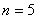 , ,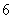 ,…布拉开(F.Brackett)系,(1922年),红外区 ,…布拉开(F.Brackett)系,(1922年),红外区
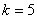 , ,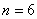 , ,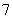 ,…普丰德(H.A.Pfumd)系,(1924年),红外区 ,…普丰德(H.A.Pfumd)系,(1924年),红外区
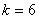 , ,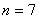 , ,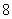 ,…哈弗莱(C.S.Humphreys)系,(1953年),红外区 ,…哈弗莱(C.S.Humphreys)系,(1953年),红外区
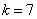 , ,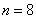 , ,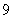 ,…汉森(Hansen)与斯特朗(Strong)系,(1973年),红外区 ,…汉森(Hansen)与斯特朗(Strong)系,(1973年),红外区
在氢谱线实验规律的基础上,里德伯、里兹(W.Ritz)等人在1890年研究其他元素(如一价碱金属)的光谱,发现碱金属光谱也可分为若干线系,其频率或波数也有和氢谱线类似的规律性,一般可用两个函数的差值来表示,函数中的参变量分别为正整数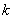 和 和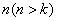
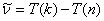
|
(13-22) |
上式称为里兹组合原理。式中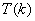 和 和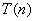 称为光谱项。对同一 称为光谱项。对同一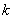 值,不同的 值,不同的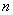 值给出同一谱系的不同谱线。对于碱金属原子,其光谱项可表示为 值给出同一谱系的不同谱线。对于碱金属原子,其光谱项可表示为
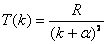 , ,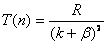 |
(13-23) |
式中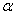 和 和 都是小于1的修正数。 都是小于1的修正数。
原子光谱线系可用这样简单的公式来表示,且其结果又非常准确,这说明它深刻地反映了原子内在的规律。 |
2.玻尔的氢原子理论 |
关于原子的结构,人们曾提出各种不同的模型,经公认肯定的是1911年卢瑟福(E.Rutherford)在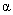 粒子散射实验基础上提出的核式结构模型,即原子是由带正电的原子核和核外作轨道运动的电子组成。根据卢瑟福提出的原子模型,电子在原子中绕核转动。这种加速运动着的电子应发射电磁波,它的频率等于电子绕核转动的频率。由于能量辐射,原子系统的能量就会不断减小,频率也将逐渐改变,因而所发射的光谱应是连续的。同时由于能量的减少,电子将沿螺线运动逐渐接近原子核,最后落在核上。因此按经典理论,卢瑟福的核型结构就不可能是稳定的系统。 粒子散射实验基础上提出的核式结构模型,即原子是由带正电的原子核和核外作轨道运动的电子组成。根据卢瑟福提出的原子模型,电子在原子中绕核转动。这种加速运动着的电子应发射电磁波,它的频率等于电子绕核转动的频率。由于能量辐射,原子系统的能量就会不断减小,频率也将逐渐改变,因而所发射的光谱应是连续的。同时由于能量的减少,电子将沿螺线运动逐渐接近原子核,最后落在核上。因此按经典理论,卢瑟福的核型结构就不可能是稳定的系统。
为了解决上述困难,1913年,玻尔(N.Bohr)在卢瑟福的核型结构的基础上,把量子化概念应用到原子系统,结合里兹并合原理,提出三个基本假设作为他的氢原子理论的出发点,使氢光谱规律获得很好的解释。
玻尔理论的基本假设是:
(1)定态假设 原子系统只能处在一系列不连续的能量状态,在这些状态中,虽然电子绕核作加速运动,但并不辐射也不吸收电磁波,这些状态称为原子系统的稳定状态(简称定态),相应的能量分别为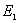 , ,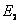 , ,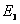 , ,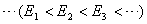 。 。
(2)频率条件 当原子从一个能量为 的定态跃迁到另一能量为 的定态跃迁到另一能量为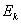 的定态时,就要发射或吸收一个频率为 的定态时,就要发射或吸收一个频率为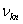 的光子 的光子
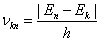 |
(13-24) |
式中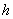 为普朗克常量。当 为普朗克常量。当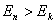 时发射光子, 时发射光子,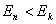 时吸收光子。式(13-24)称为玻尔频率公式。 时吸收光子。式(13-24)称为玻尔频率公式。
(3)量子化条件 在电子绕核作圆周运动中,其稳定状态必须满足电子的角动量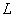 等于 等于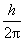 的整数倍的条件,即 的整数倍的条件,即
式中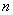 为正整数,称为量子数。式(13-25a)称为角动量量子化条件。此式也可简写成 为正整数,称为量子数。式(13-25a)称为角动量量子化条件。此式也可简写成
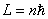 |
(13-25b) |
式中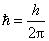 ,称为约化普朗克常量,其值等于 ,称为约化普朗克常量,其值等于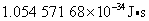 。 。
|
3.氢原子轨道半径和能量的计算 |
玻尔根据上述假设计算了氢原子在稳定态中的轨道半径和能量。他认为氢原子的核外电子在绕核作圆周运动时,其向心力就是氢原子核正电荷对轨道电子的库仑引力,应用库仑定律和牛顿运动定律得
又根据角动量量子化条件
消去两式中的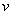 ,并以 ,并以 代替 代替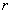 ,得 ,得
这就是原子中第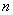 个稳定轨道的半径。由上式可知,电子轨道半径与量子数 个稳定轨道的半径。由上式可知,电子轨道半径与量子数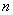 的平方成正比,其量值是不连续的。以 的平方成正比,其量值是不连续的。以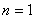 代入上式得 代入上式得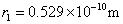 ,这是氢原子核外电子的最小轨道半径,称为玻尔半径(Bohr radius),常用 ,这是氢原子核外电子的最小轨道半径,称为玻尔半径(Bohr radius),常用 表示。这个数值和用其他方法得到的数值符合得很好。图13-16表示氢原子处于各定态时的电子轨道。 表示。这个数值和用其他方法得到的数值符合得很好。图13-16表示氢原子处于各定态时的电子轨道。
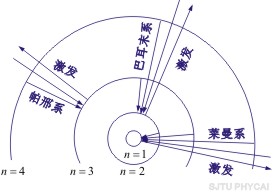
图13-16 氢原子各定态电子轨道及跃迁图
|
当电子在半径为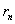 的轨道上运动时,这氢原子系统的能量 的轨道上运动时,这氢原子系统的能量 等于原子核与轨道电子这一带电系统的静电势能和电子的动能之和,如以电子在无穷远处的静电势能为零,则得 等于原子核与轨道电子这一带电系统的静电势能和电子的动能之和,如以电子在无穷远处的静电势能为零,则得
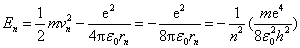 |
(13-27) |
上式表示电子在第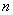 个稳定轨道上运动(即原子处于第 个稳定轨道上运动(即原子处于第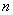 稳定态)时氢原子系统的能量。由于量子数只能取1、2、3、…等任意正整数,所以原子系统的能量是不连续的,也就是说,能量是量子化的。这种量子化的能量值称为能级。 稳定态)时氢原子系统的能量。由于量子数只能取1、2、3、…等任意正整数,所以原子系统的能量是不连续的,也就是说,能量是量子化的。这种量子化的能量值称为能级。
以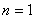 代入上式得 代入上式得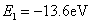 ,这是氢原子的最低能级,也称基态能级,这个能量值与用实验方法测得的氢原子电离电势符合得很好。 ,这是氢原子的最低能级,也称基态能级,这个能量值与用实验方法测得的氢原子电离电势符合得很好。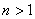 的各稳定态,其能量大于基态能量,随量子数 的各稳定态,其能量大于基态能量,随量子数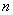 的增大而增大,能量间隔减小。这种状态称为激发态。当 的增大而增大,能量间隔减小。这种状态称为激发态。当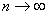 时, 时,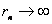 , ,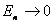 ,能级趋于连续。 ,能级趋于连续。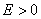 时,原子处于电离状态,能量可连续变化。图13-17表示氢原子的能级图。 时,原子处于电离状态,能量可连续变化。图13-17表示氢原子的能级图。
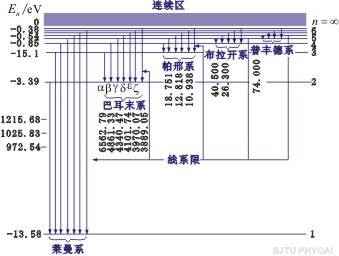
图13-17 氢原子能级图
|
用玻尔理论来研究氢原子光谱的规律,不仅能成功地说明氢原子的光谱,对类氢离子(只有一个电子绕核转动的离子,如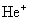 、 、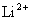 、 、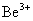 、……)的光谱也能很好地说明。由此可见,玻尔理论在一定程度上能反映单电子原子系统的客观实际。鉴于玻尔对研究原子结构和原子辐射的贡献,玻尔荣获1922年诺贝尔物理学奖。 、……)的光谱也能很好地说明。由此可见,玻尔理论在一定程度上能反映单电子原子系统的客观实际。鉴于玻尔对研究原子结构和原子辐射的贡献,玻尔荣获1922年诺贝尔物理学奖。 |
4.玻尔理论的缺陷 |
我们已经看到,玻尔理论对氢原子光谱的解释获得了很大的成功,同时玻尔关于定态的概念和光谱线频率的假设,在原子结构和分子结构的现代理论中,仍然是有用的概念。玻尔的创造性工作对现代量子力学的建立有着深远的影响。玻尔理论虽然取得一些成就,但是也存在着严重不足之处。首先,这个理论本身仍是以经典理论为基础的,而所引进的电子处于定态时不发出辐射的假设却又是和经典理论相抵触的。其次,量子化条件的引进也没有适当的理论解释。此外,由玻尔理论只能求出谱线的频率,对谱线的强度、宽度、偏振等一系列问题都无法处理。
玻尔理论的缺陷,在于处理问题没有一个完整的理论体系。例如,一方面把微观粒子(电子、原子等)看做经典力学的质点,用了坐标和轨道的概念,并且还应用牛顿定律来计算电子轨道等;另一方面又加上量子条件来限定稳定运动状态的轨道。所以玻尔理论是经典理论加上量子条件的混合物。正如当时布拉格(W.H.Bragg)对这种理论的评论时所说的那样:“好像应当在星期一、三、五引用经典规律,而在星期二、四、六引用量子规律。”这一切都反映出早期量子论的局限性。实际上,微观粒子具有比宏观粒子复杂得多的波粒二象性。正是在这一基础上,1926年薛定谔、海森伯等人建立了新的量子力学,由于量子力学能够反映微观粒子的二象性,所以成为一个完整地描述微观粒子运动规律的力学体系。 |
|