|
上面所讨论的简谐振动,振动系统都是在没有阻力作用下振动的,振幅是不随时间而变化的,就是说,这种振动一经发生,就能够永不停止地以不变的振幅振动下去。一个振动物体不受任何阻力的影响,只在回复力作用下所作的振动,称为无阻尼自由振动。这是一种理想的情况。实际上,振动物体总是要受到阻力作用的。以弹簧振子为例,由于受到空气阻力等的作用,它围绕平衡位置振动的振幅将逐渐减小,最后,终于停止下来。如果把弹簧振子浸在液体里,它在振动时受到的阻力就更大,这时可以看到它的振幅将急剧减小,振动几次以后,很快就会停止。当阻力足够大,振动物体甚至来不及完成一次振动就停止在平衡位置上了。在回复力和阻力作用下的振动称为阻尼振动。
在阻尼振动中,振动系统所具有的能量将在振动过程中逐渐减少。能量损失的原因通常有两种:一种是由于介质对振动物体的摩擦阻力使振动系统的能量逐渐转变为热运动的能量,这叫摩擦阻尼;另一种是由于振动物体引起邻近质点的振动,使系统的能量逐渐向四周辐射出去,转变为波动的能量,这叫辐射阻尼。例如音叉振动时,不仅因为摩擦而消耗能量,同时也因辐射声波而减少能量。在振动的研究中,常把辐射阻尼当作是某种等效的摩擦阻尼来处理。下面我们仅考虑摩擦阻尼这一种简单情况,在力学中我们曾经指出,流体对运动物体的阻力与物体的运动速度有关,在物体速度不太大时,阻力与速度大小成正比,方向总是和速度相反,即:
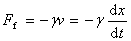
式中的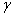 称为阻力系数,它的大小由物体的形状、大小和介质的性质来决定。 称为阻力系数,它的大小由物体的形状、大小和介质的性质来决定。
设振动物体的质量为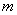 ,在弹性力(或准弹性力)和阻力作用下运动,则物体的运动方程为: ,在弹性力(或准弹性力)和阻力作用下运动,则物体的运动方程为:
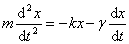
令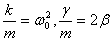 ,这里, ,这里,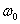 为无阻尼时振子的固有角频率, 为无阻尼时振子的固有角频率,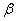 称为阻尼因子,代入上式后运动方程可改写成: 称为阻尼因子,代入上式后运动方程可改写成:
在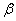 < <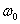 的条件下,即阻尼较小的情况,这个微分方程的解为: 的条件下,即阻尼较小的情况,这个微分方程的解为:
式中:
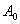 和 和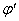 为积分常数,可由初始条件决定,上式说明阻尼振动的位移和时间的关系为两项的乘积,其中 为积分常数,可由初始条件决定,上式说明阻尼振动的位移和时间的关系为两项的乘积,其中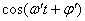 反映了在弹性力和阻力作用下的周期运动;而 反映了在弹性力和阻力作用下的周期运动;而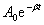 则反映了阻尼对振幅的影响。 则反映了阻尼对振幅的影响。
图10-7(a)表示阻尼振动的位移时间曲线。从图中可以看到,在一个位移极大值之后,隔一段固定的时间,就出现下一个较小的极大值,因为位移不能在每一周期后恢复原值,所以严格说来,阻尼振动不是周期运动,我们常把阻尼振动叫做准周期性运动。
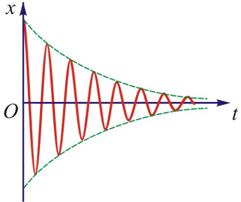
(a) 阻尼振动的位移与时间的关系 |
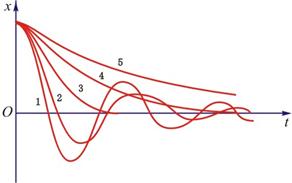
(b)不同阻尼下的阻尼振动和阻尼过大时的非周期运动 |
图 10-7 |
如果我们把振动物体相继两次通过极大(或极小)位置所经历的时向叫做阻尼振动的周期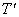 ,那么 ,那么
这就是说,由于阻尼,振动变慢了。
式(10-17)中的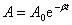 称为阻尼振动的振幅,它随着时间的增加而减小,因此阻尼振动也叫减幅振动,阻尼越小,振幅减弱越慢,每个周期内损失的能量也越少,周期也越接近无阻尼自由振动的周期,运动越接近于简谐振动;阻尼越大,振幅的减小越快(例如图10-7(b)中曲线2所示的阻尼振动,其振幅比曲线1所示的减得较快),周期比无阻尼时长得越多。 称为阻尼振动的振幅,它随着时间的增加而减小,因此阻尼振动也叫减幅振动,阻尼越小,振幅减弱越慢,每个周期内损失的能量也越少,周期也越接近无阻尼自由振动的周期,运动越接近于简谐振动;阻尼越大,振幅的减小越快(例如图10-7(b)中曲线2所示的阻尼振动,其振幅比曲线1所示的减得较快),周期比无阻尼时长得越多。
若阻尼过大,即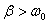 时,式(10-17)不再是式(10-16)的解,此时物体以非周期运动的方式慢慢回到平衡位置,如图10-7(b)中曲线4、5所示,这种情况称为过阻尼。若阻尼作用满足 时,式(10-17)不再是式(10-16)的解,此时物体以非周期运动的方式慢慢回到平衡位置,如图10-7(b)中曲线4、5所示,这种情况称为过阻尼。若阻尼作用满足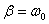 时,则振动物体将刚好能平滑地回到平衡位置,这种情况称为临界阻尼,如图10-7(b)中曲线3所示。在过阻尼状态和减幅振动状态,振动物体从运动到静止都需要较长的时间,而在临界阻尼状态,振动物体从静止开始运动回复到平衡位置需要的时间却是最短的。因此当物体偏离平衡位置时,如果要它不发生振动的情况下,最快地恢复到平衡位置,常用施加临界阻尼的方法。 时,则振动物体将刚好能平滑地回到平衡位置,这种情况称为临界阻尼,如图10-7(b)中曲线3所示。在过阻尼状态和减幅振动状态,振动物体从运动到静止都需要较长的时间,而在临界阻尼状态,振动物体从静止开始运动回复到平衡位置需要的时间却是最短的。因此当物体偏离平衡位置时,如果要它不发生振动的情况下,最快地恢复到平衡位置,常用施加临界阻尼的方法。
在生产实际中,可以根据不同的要求,用不同的方法来控制阻尼的大小。
|