1.简谐振动的表达式及其特征量
尽管振动有各种的形式,但遵从的基本规律都是相同的,在振动中,最基本、最简单的是简谐振动,其他任何复杂的振动都可以看做是简谐振动的叠加(通过傅里叶分析)。
简谐振动:物体运动时,如果离开平衡位置的位移(或角位移)按余弦函数(或正弦函数)的规律随时间变化,即:
此三角函数表述也即简谐振动的运动学方程。
振幅、周期(频率或角频率)和相位是描述简谐振动的三个重要物理量,若知道了某简谐振动的这三个量,该简谐振动就完全被确定了,故称描述简谐振动的特征量。
在振幅一定、角频率已知的情况下,振动物体在任意时刻的运动状态(位置和速度)完全取决于相位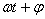 ,这从下面的分析中会看得更清楚。将式(10-1)两边对时间求一阶导数,可以得到物体振动的速度: ,这从下面的分析中会看得更清楚。将式(10-1)两边对时间求一阶导数,可以得到物体振动的速度:
|

图 10-1 |
由式(10-1)和式(10-4)两式可以看出,在振幅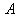 和角频率 和角频率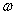 已知的情况下,振动物体的位置和速度完全由相位 已知的情况下,振动物体的位置和速度完全由相位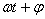 所决定。我们已经知道,位置和速度是表示一个质点在任意时刻运动状态的充分而必要的两个物理量。在振幅 所决定。我们已经知道,位置和速度是表示一个质点在任意时刻运动状态的充分而必要的两个物理量。在振幅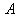 和角频率 和角频率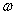 已知的情况下,振动物体在初始时刻的运动状态完全取决于初相位 已知的情况下,振动物体在初始时刻的运动状态完全取决于初相位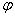 。在(10-1)和式(10-4)中令 。在(10-1)和式(10-4)中令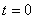 , 则分别成为下面的形式: , 则分别成为下面的形式:
式中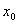 和 和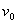 分别是振动物体在初始时刻的位移和速度, 这两个量表示了振动物体在初始时刻的运动状态, 也就是振动物体的初始条件。 分别是振动物体在初始时刻的位移和速度, 这两个量表示了振动物体在初始时刻的运动状态, 也就是振动物体的初始条件。
振幅和初相位是由初始条件决定的,由式(10-5)可得:
2.简谐振动的动力学方程
下面以弹簧振子为例来讨论简谐振动的特征及其运动规律:在一个光滑的水平面上,一质量为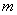 的物体系于一端固定的轻弹簧(弹簧的质量相对物体来说可以忽略不计)的自由端(这样的弹簧和物体系统就称为弹簧振子),如图10-2所示。当弹簧为原长时,物体在水平方向不受力的作用,此时物体所在的位置就是平衡位置。若将物体略加移动后释放,这时由于弹簧被拉长或被压缩,便有指向平衡位置的弹性力作用在物体上,迫使物体返回平衡位置。这样物体就在弹性力 的物体系于一端固定的轻弹簧(弹簧的质量相对物体来说可以忽略不计)的自由端(这样的弹簧和物体系统就称为弹簧振子),如图10-2所示。当弹簧为原长时,物体在水平方向不受力的作用,此时物体所在的位置就是平衡位置。若将物体略加移动后释放,这时由于弹簧被拉长或被压缩,便有指向平衡位置的弹性力作用在物体上,迫使物体返回平衡位置。这样物体就在弹性力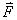 的作用下左右往返振动起来,并永远振动下去。 的作用下左右往返振动起来,并永远振动下去。
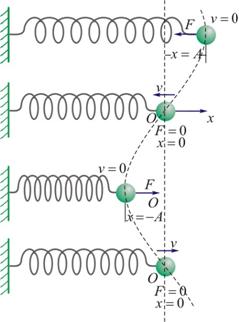
图 10-2 |
|
为了描述物体的这种运动,取物体的平衡位置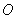 为坐标原点,物体的运动轨道为 为坐标原点,物体的运动轨道为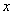 轴,向右为正。在小幅度振动的情况下,由胡克定律,物体所受的弹性力 轴,向右为正。在小幅度振动的情况下,由胡克定律,物体所受的弹性力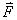 与弹簧的伸长即物体相对平衡位置的位移 与弹簧的伸长即物体相对平衡位置的位移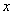 成正比,即: 成正比,即:
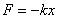
式中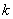 为弹簧的劲度系数,负号表示弹性力 为弹簧的劲度系数,负号表示弹性力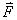 的方向与位移的方向相反。 的方向与位移的方向相反。
根据牛顿第二定律,物体的加速度为:
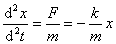
对于一个给定的弹簧振子,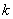 和 和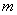 都是正值常量,令: 都是正值常量,令:
代入上式得:
或:
式(10-8)是物体的动力学方程。这个方程显示了物体受力的基本特征,即在运动过程中,物体所受力的大小与它的位移的大小成正比,而力的方向与位移的方向相反。具有这种性质的力称为线性回复力(上述的动力学方程还可以从能量关系得到)。
在上面我们以弹簧振子为例分析了简谐振动,但在实际发生的振动大多较为复杂:(1)回复力不是弹力,而是重力、浮力等;(2)不是线性力。但在一定条件下,可以近似地当成线性回复力,如单摆、复摆等。 |
|
3.简谐振动运动学方程的三种表示法
除了在前面我们介绍的简谐振动运动学方程三角函数法外,通常还有另外两种表示,即:(1)复指数法,(2)旋转矢量法。我们这里着重介绍旋转矢量法。
所谓旋转矢量法即把简谐振动用一个旋转矢量来描绘。在坐标系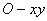 中,以坐标原点 中,以坐标原点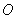 为始端,末端为 为始端,末端为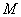 点作一矢量 点作一矢量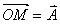 ,如图10-3所示。令 ,如图10-3所示。令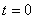 时 时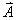 与 与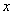 轴的夹角为 轴的夹角为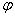 ,以匀角速度 ,以匀角速度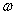 ,半径为 ,半径为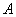 绕坐标原点 绕坐标原点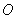 作逆时针方向匀速转动,在 作逆时针方向匀速转动,在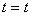 时, 时,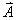 与 与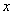 轴的夹角等于相位 轴的夹角等于相位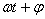 ,则矢量 ,则矢量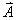 末端 末端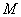 在 在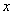 轴上的投影点 轴上的投影点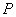 的位移是: 的位移是: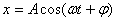 ,这正是简谐振动的运动学方程。由于矢量 ,这正是简谐振动的运动学方程。由于矢量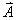 在转动过程中,末端 在转动过程中,末端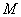 点作匀速圆周运动,故通常把这个圆称为参考圆。矢量 点作匀速圆周运动,故通常把这个圆称为参考圆。矢量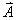 转一周所需的时间就是简谐振动的周期。 转一周所需的时间就是简谐振动的周期。
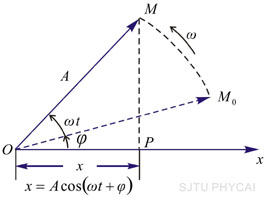
图 10-3 |
|
由此可见,旋转矢量法能直观的反映简谐振动的三个特征量振幅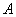 、角频率 、角频率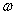 、相位 、相位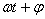 的物理含义,且为振动的叠加提供最间接的方法。 的物理含义,且为振动的叠加提供最间接的方法。
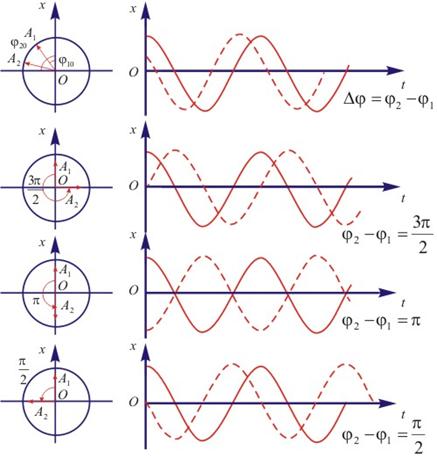
图 10-5 |
4.简谐振动的能量
现在仍以水平弹簧振子为例来讨论作简谐振动的系统的能量。此时系统除了具有动能以外,还具有势能。振动物体的动能为:
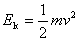
如果取物体在水平位置的势能为零,则弹性势能为:

由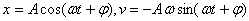 代入得: 代入得:
上述式子表明:物体作简谐振动时,其动能和势能都是随时间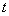 作周期性变化,位移最大时,势能达最大值,动能为零;物体通过平衡位置时,势能为零,动能达最大值。 作周期性变化,位移最大时,势能达最大值,动能为零;物体通过平衡位置时,势能为零,动能达最大值。
动能和势能的变化频率是弹簧振子振动频率的两倍(如图10-6所示)。由于在运动过程中,弹簧振子不受外力和非保守内力的作用,其总能量守恒,另考虑到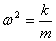 ,系统总能量为 ,系统总能量为
|
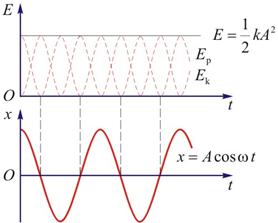
图 10-6 |
上式表明:谐振系统在振动过程中的动能和势能虽然分别随时间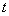 作周期性变化,但总的机械能在振动过程中是一个常量。简谐振动系统的总能量和振幅的平方成正比,这一结论对任何谐振系统都是正确的。 作周期性变化,但总的机械能在振动过程中是一个常量。简谐振动系统的总能量和振幅的平方成正比,这一结论对任何谐振系统都是正确的。
|