我们在前面多次提到电场和磁场是一个统一的整体,静止电荷的静电场和恒定电流的磁场只不过是电磁场的两种特例。我们最初认识了电场,接着又认识了磁场,最后才从两者的相互联系进一步认识到统一的电磁场的存在。为了更清楚地说明电磁场的统一性,我们可以从运动的相对性进行考察。如果在某参考系中有一静止电荷,那么相对于这个参考系静止的观察者通过实验考察,将发现在电荷周围只存在静电场。但是对于相对于上述参考系作匀速直线运动的观察者来说,这电荷相对于他正在作匀速运动,从而形成了电流,因此这个观察者将发现在电荷周围既有电场又有磁场。也许大家要奇怪地问:在电荷周围究竟存在着什么?回答是肯定的,即存在着电磁场。至于有些人只观测到电场,而另一些人则观测到电场和磁场都存在,那是由于电荷相对人们的运动情况不同,因此认识的侧面也就不同,但正是这些不同的侧面反映了电磁场的统一性和相对性。
上述事实告诉我们,电场和磁场本身具有相对的意义,为了描述电磁运动,首先要选定参考系。事实上,前面各章所讨论的电磁运动,都应理解为是在某确定的参考系内观察和研究的。在本书第四章中我们曾讲过,根据相对性原理,在任何惯性系内,一切物理规律是相同的,电磁场理论的基本方程——麦克斯韦方程组也遵守这一原理,即从一个惯性系K变换到另一个惯性系K′ 时,在洛伦兹变换下保持不变。
式中
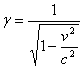
只要把上式中的 换成 换成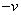 就可以得到反变换式。 就可以得到反变换式。
在不同的惯性系中采用各自所在系统的时间、空间及场量来描述电磁现象,即描述电磁现象的场量在不同惯性系内可以有不同的量值,说明电磁场量是相对的;但是每一个惯性系中电磁场量之间的关系都有相同的麦克斯韦方程组形式,说明电磁规律是绝对的。
仍以图9-30所示的情况为例来讨论上述场量变换关系的具体应用。假如电荷q静止于惯性系K′ 的原点处,那么在K′ 系中仅观察到电场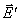 ,并在t′ 时刻测得 ,并在t′ 时刻测得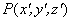 处的电磁场为 处的电磁场为
其电场线以点电荷为中心,在各个方向均匀分布,图9-31(a)表示在K′ 系中电场线在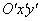 平面内的分布情况,而磁场则为零。 而K′ 系相对于惯性系K 以速度 平面内的分布情况,而磁场则为零。 而K′ 系相对于惯性系K 以速度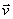 沿Ox轴方向运动,所以在K系内观察,点电荷q是以速度 沿Ox轴方向运动,所以在K系内观察,点电荷q是以速度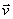 沿Ox轴方向运动的,除电场外还观察到磁场(图9-32)。由上述场量的变换关系,可得t时刻在点 沿Ox轴方向运动的,除电场外还观察到磁场(图9-32)。由上述场量的变换关系,可得t时刻在点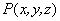 处的电磁场为 处的电磁场为
现在再利用空间坐标的洛伦兹变换式,将式(9-39)中的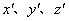 及 及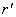 用K系中的相应坐标来表示, 用K系中的相应坐标来表示,
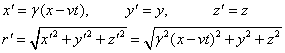
一并与式(9-39)代入式(9-40)便得
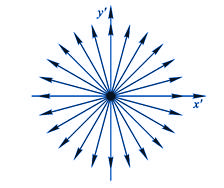
(a)点电荷在静止或低速下的电场线分布 |
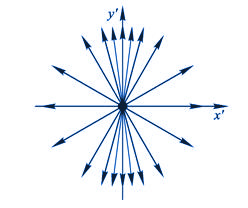
(b)点电荷在高速下的电场线分布 |
图 9-31 点电荷在不同状态下测得的电场线分布 |
从上述结果可知,在K系内电场分布已经不具有球形对称性,平行于电荷运动方向的场强分量小于电荷静止时的场强,而垂直于运动方向的平面内的场强分量则大于电荷静止时的场强,并且随着电荷运动速度的增加,电场趋向于集中分布在垂直于运动方向的平面内(图9-31(b))。至于磁场在空间的分布情况,其磁感应线分布在垂直于运动方向的平面内,是以电荷运动方向为中心线的同心圆,磁感应线的方向和运动正电荷的运动的方向仍服从右手螺旋法则(图9-32)。
|
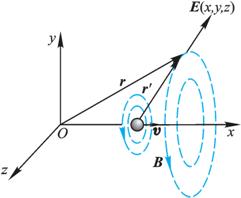
图 9-32 电荷在K系内的场强 |
总之,电磁场量的洛伦兹变换式以及上面这个实例不仅说明了在不同惯性系中电场和磁场的相对性(在不同惯性系中根据电荷的运动有不同的测量值),而且更说明了电场与磁场的不可分割性,电场的变换式中包含了磁场分量;磁场的变换式中包含有电场分量。电磁场是一统一的实体。
事实上,由式(9-40)我们还可以很直接地看到电场与磁场的关联性。将式(9-40a)式代入到(9-40b)式,可以得到
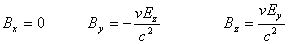
将它们合起来写,即为矢量关系式
此式反映了电荷以任何速度运动时所建立的电场与磁场的关系,设电荷运动的速度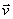 与电场强度 与电场强度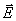 方向的夹角为θ,那么磁场 方向的夹角为θ,那么磁场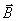 的大小为 的大小为
设电荷经过K 系原点的时刻为t=0,按式(9-41)可以确定空间各点的电场强度的大小为
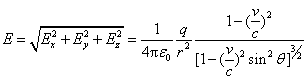
以此代入式(9-43),并考虑到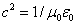 ,得 ,得
当电荷运动的速度较低时,即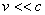 ,上式可简化为 ,上式可简化为
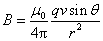
写成矢量式
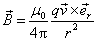
与(8-24)式一致,正是运动电荷产生的磁场。
|