例题7-6-1  两个半径分别为R和r的球形导体(R＞r)，用一根很长的细导线连接起来(如图)，使这个导体组带电，电势为V，求两球表面电荷面密度与曲率的关系。

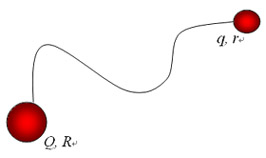论证带电导体上的电荷面密度与曲率的关系

解：两个导体所组成的整体可看做是一个孤立导体系。设这两个球相距很远，使每个球面上的电荷分布在另一球处所激发的电场可以忽略不计。细线的作用是使两球保持等电势，而细线上少量的电荷在两球处所激发的电场影响也可以忽略。因此，每个球又可近似地看做为孤立导体，在两球表面上的电荷分布各自都是均匀的。设大球所带电荷量为Q，小球所带电荷量为q，在静电平衡时它们有相等的电势值，为

        
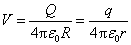
    得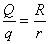         
    可见大球所带电荷量Q比小球所带电荷量q多。因为两球的电荷面密度分别为

        
    所以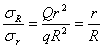           

可见电荷面密度和曲率半径成反比，即曲率半径愈小(或曲率愈大)，电荷面密度愈大。 当两球相距不远时，两球所带电荷的相互影响不能忽略，这时每个球都不能看做是孤立导体，两球表面上的电荷分布也不再均匀。于是，同一球面上各处的曲率虽相等，而电荷面密度却不再相同。因此，电荷面密度与曲率半径成反比仅对孤立导体成立。