例题2-7-1 按经典原子理论,认为氢原子中的电子在圆形轨道上绕核运动。电子与氢原子核之间的静电力为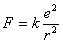 ,其中 ,其中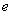 为电子或氢原子核的电荷量, 为电子或氢原子核的电荷量,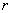 为轨道半径, 为轨道半径,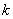 为常量。因为电子的角动量具有量子化的特征,所以电子绕核运动的角动量只能等于 为常量。因为电子的角动量具有量子化的特征,所以电子绕核运动的角动量只能等于 的整数( 的整数(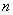 )倍[ )倍[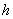 是一常数,叫做普朗克(M. Planck)常量],问电子运动容许的轨道半径等于多少? 是一常数,叫做普朗克(M. Planck)常量],问电子运动容许的轨道半径等于多少?
解: 设电子的质量为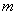 ,绕原子核运动的圆轨道半径为 ,绕原子核运动的圆轨道半径为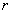 ,速度为 ,速度为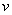 ,那么电子的向心加速度 ,那么电子的向心加速度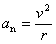 。由于作用在电子上的向心力就是原子核对电子的静电引力,于是由牛顿第二定律得 。由于作用在电子上的向心力就是原子核对电子的静电引力,于是由牛顿第二定律得
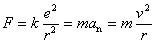 (1) (1)
由于电子绕核运动时,角动量具有量子化的特征,即
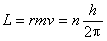 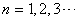 (2) (2)
由式(1)和式(2)两式,得
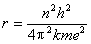 (3) (3)
由上式可知,电子绕核运动容许的轨道半径与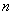 平方成正比。这就是说,只有半径等于一些特定值的轨道才是容许的,轨道半径的量值是不连续的。 平方成正比。这就是说,只有半径等于一些特定值的轨道才是容许的,轨道半径的量值是不连续的。
将各常量的值代入式(3),并取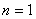 ,得最小的 ,得最小的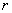 值: 值:
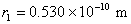
从原子物理学中知道,这一量值与用其他方法估计得到的量值符合得很好。
|