在机械运动范围内的能量,除了动能外,还有势能。在生活和生产的实践中我们知道,从高处落下的重物能够做功。我们把这种能量叫做重力势能。因为重力是地球对物体的作用,同时一般物体所处的高度总是相对于地面来说的,所以重力势能既和物体与地球间的相互作用有关,又和这二者的相对位置有关。
从重力是保守力的特点来看,重力做功导致了作为位置函数的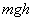 项的出现。因为功 项的出现。因为功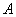 是能量变化的量度,所以应把 是能量变化的量度,所以应把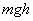 理解为和位置有关的能量,而这就是我们所说的重力势能。一般用 理解为和位置有关的能量,而这就是我们所说的重力势能。一般用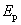 表示势能。 表示势能。
对处于弹性形变状态的物体,也具有能量。我们把这种能量叫做弹性势能。和重力势能相似,弹性势能和物体各部分之间相互作用有关,又和这些部分的相对位置有关。对引力做功,我们同样可引入引力势能的概念。
保守力的功与路径无关的性质,大大简化了保守力做功的计算。引入势能概念以后,我们约定:在保守力场中,物体在位置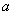 , ,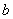 的势能 的势能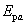 , , 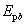 之差等于由 之差等于由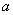 移动到 移动到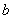 过程中保守力的功 过程中保守力的功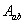 。即 。即
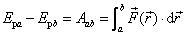
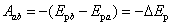
上式表明,系统在由位置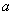 改变到位置 改变到位置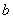 的过程中,成对保守内力的功等于系统势能的减少(或势能增量的负值)。 的过程中,成对保守内力的功等于系统势能的减少(或势能增量的负值)。
由此可得,
重力做功 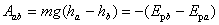
弹性力做功 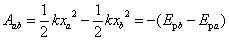
万有引力做功 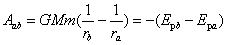
我们可以分别引入:
重力势能 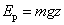 (选取势能零点: (选取势能零点: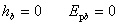 ) )
弹性势能 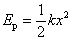 (选取势能零点: (选取势能零点: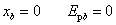 ) )
引力势能 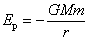 (选取势能零点: (选取势能零点: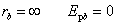 ) )
说明:
(1)并非所有力做功都能引入势能。
(2)势能是属于相互作用有保守力的物体系统的。
(3)势能的大小只有相对的意义。
(4)物体系统的势能差是绝对的,与势能零点的选取无关。 |